Question

The area of the region enclosed by the curve $y=x$, $x=e$, $y=\dfrac{1}{x}$ and the positive x-axis is:
A. ${}^{1}/{}_{2}$ square units
B. $1$ square units
C. ${}^{3}/{}_{2}$ square units
D. ${}^{5}/{}_{2}$ square units

Answer 1

The relation $y=\dfrac{1}{x}$ or $xy=1$ is representing a hyperbola and x and y are in reverse relation i.e. if y increases then x will decrease and vice versa. So use this information to represent the curve $y=\dfrac{1}{x}$ or $xy=1$. Integration of $\dfrac{1}{x}$ is given as $\int{\dfrac{1}{x}}dx=\log {{e}^{x}}$.

Complete step by step answer:
Given curves in the problem are $y=x$, $x=e$, $y=\dfrac{1}{x}$ and positive x-axis.
To find the area bounded by these curves, we need to draw a neat diagram showing all the curves on the coordinate axes. So, as $y=x$ and $x=e$ are the straight lines, where $y=x$ will pass through origin will slope of 1 (by comparing it with equation of straight line, $y=mx+c$) and line $x=e$ will pass through (e, 0) parallel to the y-axis. So we need to observe the curve $y=\dfrac{1}{x}$ only.
We can rewrite the equation $y=\dfrac{1}{x}$ as $xy=1$ as well, which is representing a rectangular hyperbola in all four quadrants. Hence, the diagram can be given as,

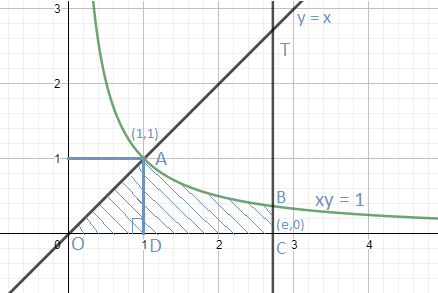
As intersection $xy=1$ and $y=x$, can be given as,
x = 1, y = 1, i.e. point A.
The shaded region in the above diagram is the bounded area represented by all the curves given in the question.
Hence we need to determine the area of OABC, and by the observation, we get that the area of OABC can be calculated by the sum of area of triangle OAD and region ABCD.
As we know the length of OD and AD is given as, OD = 1, AD = 1.
Area of a triangle is given as $=\dfrac{1}{2}\times base\times height....(1)$
Hence we get area of OAD $=\dfrac{1}{2}\times 1\times 1=\dfrac{1}{2}uni{{t}^{2}}....(2)$
We can calculate the area of ABCD by integrating the curve $y=\dfrac{1}{x}$ from $x=1$ to $x=e$.
Hence area of ABCD $=\int\limits_{1}^{e}{\dfrac{1}{x}}dx$.
As we know, $\int{\dfrac{1}{x}dx}=\log {{e}^{x}}$.
So we get area of ABCD $=\int\limits_{1}^{e}{\dfrac{1}{x}}dx=\left( {{\operatorname{loge}}^{x}} \right)_{1}^{e}=\left( {{\log }_{e}}e-{{\log }_{e}}1 \right)$.
We know that the property of logarithm function that value of ${{\log }_{a}}a=1$ and value of ${{\log }_{e}}1=0$.
Hence we get,
Area of ABCD = 1 – 0 = 1 unit…..(3)
Hence the area of OABC can be calculated by adding the area of OAD and ABCD from equation (2) and (3). So we get,
Area of OABC = $1+\dfrac{1}{2}=\dfrac{3}{2}uni{{t}^{2}}$.
Hence the area bounded by the given curves in the problem is $\dfrac{3}{2}uni{{t}^{2}}$.
Option C is the correct answer.

Note:
Curve $xy=1$ is a rectangular hyperbola because the expression $xy=1$ or $x=\dfrac{1}{y}$ has an inverse relation in x and y. So if x increases, then y will decrease and vice-versa. That’s why the curves in all 4 quadrants have an inverse relation. One may easily understand the curve of $xy=1$ by this approach.
Diagrams play an important role for this type of question.
Another approach for getting area of bounded region from the diagram would be given as,
Area of shaded region = area of triangle OTC – area of TAB
where, we need to calculate area of TAB by difference of area of DATC and area of DABC. So it can be another approach.