Solveeit Logo
Login

Question

Question: The area of the region bounded by \(y = x\) and \(y = {x^2}\) is A. \(\dfrac{2}{3}\) B. \(\dfra...

The area of the region bounded by y=xy = x and y=x2y = {x^2} is
A. 23\dfrac{2}{3}
B. 12\dfrac{1}{2}
C. 13\dfrac{1}{3}
D. 16\dfrac{1}{6}

Explanation

Solution

According to the question given in the question we have to determine the region bounded by y=xy = x and y=x2y = {x^2}. So, first of all we have to determine the values of coordinates of point P as mentioned in the diagram, given below:

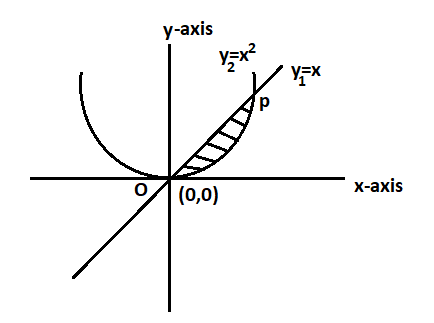
Now, we can obtain the coordinates or point of x so, we have to substitute the value of x in the expression to find the required area.
Now, to find the required area we have to find the integration with the limit from 0 to 1 and after finding the integration we can obtain the area required.

Formula used: ∫xdx=x22+c..................(A)\int {xdx = \dfrac{{{x^2}}}{2} + c..................(A)}

Complete Step by Step Solution:
Step 1: First of all to find the coordinates of point P we have to substitute the value of y in the given expression as mentioned in the solution hint and we can also understand it with the help of diagram as mentioned below:

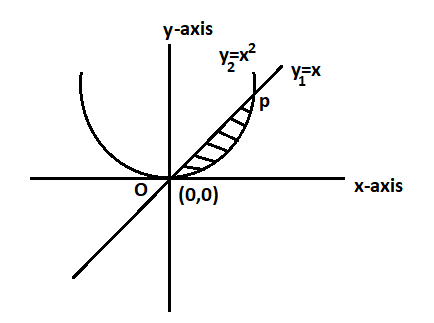
⇒x2=x\Rightarrow {x^2} = x
Now, on solving the expression obtained just above,
⇒x=0,1\Rightarrow x = 0,1
Step 2: As we have obtained the value of x=0x = 0 which corresponds to origin as mentioned in the diagram in step 1 O(0,0) and for p we have to put x = 1
Step 3: Now, to obtain the required area we have to find the integration from 0 to 1 as mentioned in the solution hint. Hence,
A=∫01(y1−y2)dxA = \int\limits_0^1 {({y_1} - {y_2}} )dx
Step 4: Now, on substituting the values of the given expressions y=xy = x and y=x2y = {x^2}. In the expression as obtained in the solution step 3. Hence,
=∫01x−x2dx= \int\limits_0^1 {x - {x^2}} dx
Now, to solve the integration as obtained just above we have to apply the formula (A) as mentioned in the solution hint.

=[x22−x33]01 =[12−13−0] =3−26 =16 = \left[ {\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{3}} \right]_0^1 \\\ = \left[ {\dfrac{1}{2} - \dfrac{1}{3} - 0} \right] \\\ = \dfrac{{3 - 2}}{6} \\\ = \dfrac{1}{6}

Hence, with the help of formula (A) as mentioned in the solution hint we have obtained the required area which is =16 = \dfrac{1}{6}.

Therefore correct option is (D)

Note: To find the required area it is necessary to find the coordinates of point P so that we can determine the area covered by the lines y=xy = x and y=x2y = {x^2}
Integration is the best way to determine the area of undefined shapes by substituting the values of the limits obtained.