Question

The area of the region bounded by the parabola $y={{x}^{2}}-3x$ with $y\le 0$ is
(A) $3$
(B) $-3$
(C) $-\dfrac{9}{2}$
(D) $\dfrac{9}{2}$

Answer 1

Hint: The parabola is also a quadratic in $x$. Imagine if the curve will be concave upward or concave downward by analysing the coefficient of ${{x}^{2}}$. Next, try to find where the curve cuts the $x$ axis. Every value of $y$ below the $x$ axis will be negative, and if the curve is concave upward, then the portion of the curve enclosed between the two roots will definitely lie below the $x$ axis, and thus, this will be our required area.

Complete Step-by-Step Solution:
First, let’s try visualising the function given to us.
This is a parabola, but it also looks like a quadratic equation in $x$. This means that there might be two places where this equation might cut the $x$ axis. The fact that the curve cuts the $x$ axis implies that at these points, the value of $y$ is zero. So, first of all let’s try finding out the places where $y=0$ for this curve.
Therefore, substituting 0, for $y$, we get :
$\begin{aligned} & {{x}^{2}}-3x=y \\\ & \Rightarrow {{x}^{2}}-3x=0 \\\ & \Rightarrow x(x-3)=0 \\\ & \Rightarrow x=0,3 \\\ \end{aligned}$
Hence, the curve cuts the $x$ axis at the points $(0,0)$ and $(3,0)$.
Now, let’s try visualising the curve properly. The coefficient of ${{x}^{2}}$ in the equation is positive, which means that this parabola is concave upwards, or it looks like a bowl. Now, the information we have says that it looks like a bowl and it cuts the $x$ axis at 0 and 3. Using this, we can say that between 0 and 3, the function must take on negative values of $y$, and hence, for this function, $y\le 0$ means that $x\in (0,3)$.
Hence, we can now find the area by integrating the function from $x=0$to $x=3$.
The formula of finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
Since in this sum, the entire area in question lies below the $x$ axis, and will be negative, we don’t need to break the integral further, so that all the area is positive. We can simply take the modulus of the entire integral.
Therefore, for our required area, $f(x)={{x}^{2}}-3x$, $a=0$ and $b=3$.
Therefore, substituting these values into the formula, we get :
$\begin{aligned} & |\int\limits_{a}^{b}{f(x)dx|}=|\int\limits_{0}^{3}{({{x}^{2}}-3x)dx|=|[\dfrac{{{x}^{3}}}{3}-3\dfrac{{{x}^{2}}}{2}]_{0}^{3}|=|(\dfrac{27}{3}-\dfrac{27}{2})-(0-0)|} \\\ & =27|\dfrac{1}{3}-\dfrac{1}{2}| \\\ & =27\times \dfrac{1}{6}=\dfrac{9}{2} \\\ \end{aligned}$
Here is a diagram of what we imagined above.

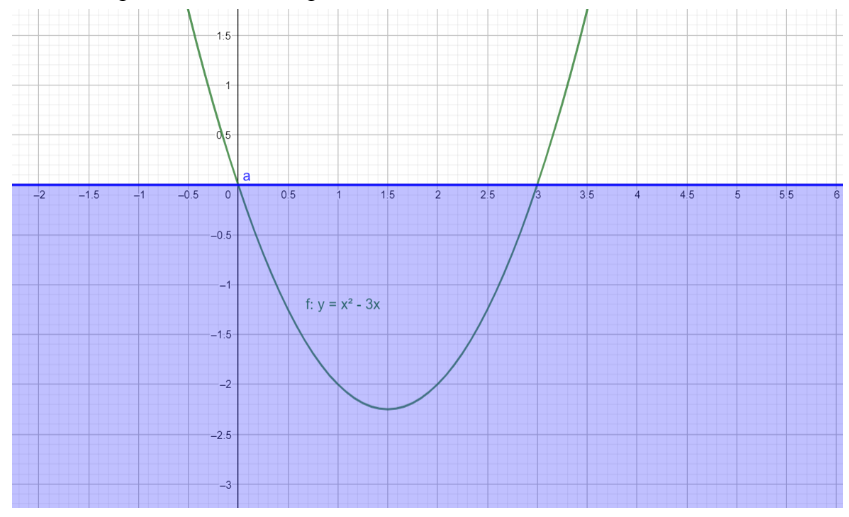
Here, the violet region is the region where $y$ is non positive, and the graph of $y={{x}^{2}}-3x$ is shown in green. As you can see clearly, the graph is indeed concave upward, and cuts the $x$ axis at $x=0$ and $x=3$. Thus, the entire area enclosed by the curve for $y\le 0$, is also bound between $x=0$ and $x=3$.

Hence, our required area is $\dfrac{9}{2}$.