Question

The area of the region bounded by the curves $y={{x}^{2}}$and $y=16.$
A.$\dfrac{128}{3}sq.units$
B.$\dfrac{64}{3}sq.units$
C.$\dfrac{32}{3}sq.units$
D.$\dfrac{256}{3}sq.units$

Answer 1

Hint- Draw both curves to determine the region. After that, find common points of intersection of curve and line. Then use integral in order to find the area.

Complete step-by-step answer:
First draw $y={{x}^{2}}$, which is a parabola (opens upwards) then draw $y=16$ which is line parallel to the x axis and having distance 16 units from the origin.

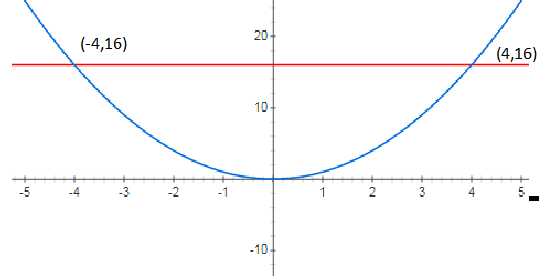
The required area of region is,
$\int\limits_{0}^{16}{2(\sqrt{y}-0)dy=2.\dfrac{2}{3}{{[{{y}^{\dfrac{3}{2}}}]}_{0}}^{16}}$
$=\dfrac{256}{3}sq.units$
The area of the required region is $\dfrac{256}{3}sq.units$.
Option (D) is correct.

Note- Here, the bounded area is symmetric about the x axis that’s why we have multiplied by 2 to the other half region to get the required area.