Question
Question: The area of the region above the x-axis bounded by the curve \[y = \;tanx\], \[0 \leqslant x \leqsla...
The area of the region above the x-axis bounded by the curve y=tanx, 0⩽x⩽2π and the tangent to the curve at x=4π is
(A) 21(log2−21)
(B) 21(log2+21)
(C) 21(1−log2)
(D) 21(1−log2)
Solution
Here we will first find the equation of the tangent using the slope point form i.e.
y−y1=dxdy(x−x1) and then we will find the coordinate where the tangent cuts the x axis and then we will finally find the area of the shaded region.
Complete step-by-step answer:
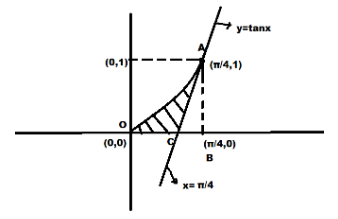
First of all we will find the equation of the tangent which is passing through (4π,1)
Now we know that for any curve tangent is passing through a point (x1,y1), then the equation of tangent using slope point form is given by:-
y−y1=dxdy(x−x1)…………………………………..(1)
Hence we need to find dxdy at x=4π
Now since y=tanx
Differentiating it both the sides we get:-
dxdy=dxd(tanx)
Now as we know that:-
dxd(tanx)=sec2x
Hence putting in the value we get:-
dxdy=sec2x
Now since we have calculate its value at x=4π
Therefore substituting x=4π in above equation we get:-
dxdy=sec2(4π)
Now since we know that:-
sec(4π)=2
Hence putting the value in above equation we get:-
dxdy=(2)2
Solving it further we get:-
dxdy=2
Now putting this value and the values of passing points in equation 1 we get:-
y−1=2(x−4π)
Simplifying it we get:-
y−1=2x−2π
Therefore the equation of tangent is:-
y−1=2x−2π
Now we will find the point where the tangent is touching the x axis.
Therefore, this implies y=0
Hence putting y=0 in the equation of tangent we get:-
0−1=2x−2π
Now evaluating for x we get:-
2x=2π−1
Dividing the equation by 2 we get:-
x=4π−21
Hence the point where tangents cuts the x axis is (4π−21,0)
Now we will find the area of the shaded region.
Area of shaded region=area under the curve y=tanx- area under the tangent
Therefore, we get:-
required area=∫04πtanxdx−area of triangle ABC……………………….(2)
Now we know that area of triangle is given by:-
area=21×base×height
In triangle ABC
Also,
height=1
Hence putting these values in formula of area we get:-
area=21×21×1
Solving it further we get:-
area=41
Also, we know that:-
∫tanxdx=log(secx)+C
Hence putting the respective values in equation 2 we get:-
required area=[logsecx]04π−41
Solving it further and putting the limits we get:-
required area=(logsec(4π)−logsec(0))−41
Now we know that:-
sec(4π)=2
sec0=1
Hence putting these values we get:-
required area=[log2−log1]−41
We know that:-
log1=0
Therefore putting the value we get:-
required area=[log2−0]−41
We know that:-
logxn=nlogx
Hence applying this property we get:-
Simplifying it we get:-
required area=21[log2−21]sq units
Hence option A is the correct option.
Note: Students should note that area under the curve is the area between the two curves.
Students might make mistake in integration so, they should keep in mind the following formula:
∫tanxdx=log(secx)+C
Also, the limits should be substituted carefully.
