Question

The area of the region $A=\left[ \left( x,y \right):0\le y\le x\left| x \right|+1\text{ and }-1\le x\le 1 \right]$ in square units is
$\begin{aligned} & \left( A \right)\dfrac{2}{3} \\\ & \left( B \right)\dfrac{1}{3} \\\ & \left( C \right)2 \\\ & \left( D \right)\dfrac{4}{3} \\\ \end{aligned}$

Answer 1

We solve the given question by dividing the curve into two parts, one is when x is less than zero and one is when x is greater than zero. Then we plot the graph of the given curves and find the region for which we need to calculate the area. Then we integrate the curves and add them to get the final area of the region bounded by them using the formula $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}$.

Complete step-by-step solution:
We are given the curves, $-1\le x\le 1$ and $0\le y\le x\left| x \right|+1$.
Consider the second curve, $0\le y\le x\left| x \right|+1$.
Let us consider the function $f\left( x \right)=\left| x \right|$. It can be written as
\left| x \right|=\left\\{ \begin{matrix} x\text{ when }x>0 \\\ -x\text{ when }x< 0 \\\ \end{matrix} \right.
So, by using that we get,
When $x<0$, the equation transforms as $0\le y\le -{{x}^{2}}+1$, that is $0\le y\le 1-{{x}^{2}}$.
When $x>0$, the equation transforms as $0\le y\le {{x}^{2}}+1$.
So, now let us plot the graph of the given regions,

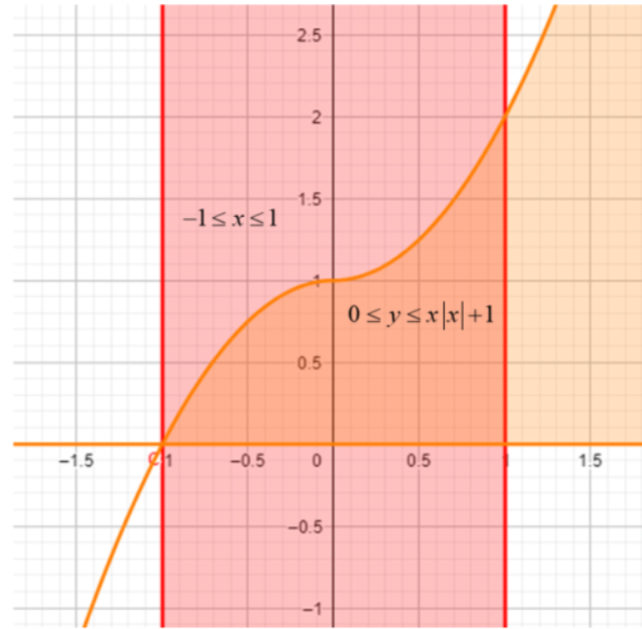
The area common to both the curves is the region between the curve and x-axis between x=-1 and x=1. Here between x=-1 and x=0, the curve is $y=-{{x}^{2}}+1$ and between x=0 and x=1 the curve is $y={{x}^{2}}+1$.
Now let us find the area using integration.
Area of required region is
$\begin{aligned} & \Rightarrow \int\limits_{-1}^{0}{\left( -{{x}^{2}}+1 \right)dx}+\int\limits_{0}^{1}{\left( {{x}^{2}}+1 \right)dx} \\\ & \Rightarrow \left[ -\dfrac{{{x}^{3}}}{3}+x \right]_{-1}^{0}+\left[ \dfrac{{{x}^{3}}}{3}+x \right]_{0}^{1} \\\ & \Rightarrow \left[ \left( -\dfrac{{{0}^{3}}}{3}+0 \right)-\left( -\dfrac{{{\left( -1 \right)}^{3}}}{3}+\left( -1 \right) \right) \right]+\left[ \left( \dfrac{{{1}^{3}}}{3}+1 \right)-\left( \dfrac{{{0}^{3}}}{3}+0 \right) \right] \\\ & \Rightarrow \left[ 0-\left( -\dfrac{-1}{3}-1 \right) \right]+\left[ \left( \dfrac{1}{3}+1 \right)-0 \right] \\\ & \Rightarrow \left[ 0-\left( -\dfrac{2}{3} \right) \right]+\left[ \dfrac{4}{3} \right] \\\ & \Rightarrow \dfrac{2}{3}+\dfrac{4}{3} \\\ & \Rightarrow \dfrac{6}{3} \\\ & \Rightarrow 2 \\\ \end{aligned}$
So, area of our required region is 2 square units.
Hence answer is Option C.

Note: The major mistake one does while solving this question is one might forget to convert the $\left| x \right|$ present in the equation of the curve, $0\le y\le x\left| x \right|+1$. One might forget to convert $\left| x \right|$ and write the curve as $0\le y\le {{x}^{2}}+1$. But it is correct only when x is greater than zero not when x is less than zero. So, we should convert $\left| x \right|$ and write the curve as $0\le y\le 1-{{x}^{2}}$ when x is less than zero and $0\le y\le {{x}^{2}}+1$ when x is greater than zero.