Solveeit Logo
Login

Question

Question: The area of the parallelogram whose diagonals represent the vectors \(3\overrightarrow{i}+\overright...

The area of the parallelogram whose diagonals represent the vectors 3i→+j→−2k→3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k} and i→−3j→+4k→\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k} is.
(a) 10310\sqrt{3}
(b) 535\sqrt{3}
(c) 88
(d) 44

Explanation

Solution

Hint: For solving this question we will use the concept that if ACAC and BDBD are the diagonals of a quadrilateral, then its vector area is 12(AC→×BD→)\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right) . After that, we will find the cross product of the given vectors and multiply its magnitude by 0.5 to find the value of the area of the parallelogram easily.

Complete step-by-step solution -
Given:
It is given that vectors 3i→+j→−2k→3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k} and i→−3j→+4k→\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k} are the diagonals of a parallelogram and we have to find its area.
Now, here before we proceed we should know that if ACAC and BDBD are the diagonals of a quadrilateral, then its vector area is 12(AC→×BD→)\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right) . For more clarity look at the figure given below:

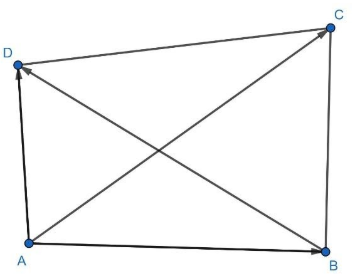
Now, in the above figure consider the ΔABD\Delta ABD and apply the triangle law of vector addition. Then,
AB→+BD→=AD→ ⇒BD→=AD→−AB→...............(1) \begin{aligned} & \overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD} \\\ & \Rightarrow \overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}...............\left( 1 \right) \\\ \end{aligned}
Now, as we know that the vector area of any triangle is equal to half of the cross product of any two adjacent side vectors. Then,
Vector area of the quadrilateral ABCD= Vector area of ΔABC+ Vector area of ΔACD ⇒Vector area of the quadrilateral ABCD=12(AB→×AC→)+12(AC→×AD→) ⇒Vector area of the quadrilateral ABCD=−12(AC→×AB→)+12(AC→×AD→) ⇒Vector area of the quadrilateral ABCD=12(AC→×(AD→−AB→)) \begin{aligned} & \text{Vector area of the quadrilateral }ABCD=\text{ Vector area of }\Delta ABC+\text{ Vector area of }\Delta ACD \\\ & \Rightarrow \text{Vector area of the quadrilateral }ABCD=\dfrac{1}{2}\left( \overrightarrow{AB}\times \overrightarrow{AC} \right)+\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{AD} \right) \\\ & \Rightarrow \text{Vector area of the quadrilateral }ABCD=-\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{AB} \right)+\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{AD} \right) \\\ & \Rightarrow \text{Vector area of the quadrilateral }ABCD=\dfrac{1}{2}\left( \overrightarrow{AC}\times \left( \overrightarrow{AD}-\overrightarrow{AB} \right) \right) \\\ \end{aligned}
Now, substitute BD→=AD→−AB→\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB} from equation (1) in the above equation. Then,
Vector area of the quadrilateral ABCD=12(AC→×(AD→−AB→)) ⇒Vector area of the quadrilateral ABCD=12(AC→×BD→) \begin{aligned} & \text{Vector area of the quadrilateral }ABCD=\dfrac{1}{2}\left( \overrightarrow{AC}\times \left( \overrightarrow{AD}-\overrightarrow{AB} \right) \right) \\\ & \Rightarrow \text{Vector area of the quadrilateral }ABCD=\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right) \\\ \end{aligned}
Now, to get the magnitude of the area of the quadrilateral ABCDABCD we have to find the magnitude of the vector 12(AC→×BD→)\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right) .
Now, we come back to our question in which we have to find the area of the parallel gram whose diagonals represent the vectors 3i→+j→−2k→3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k} and i→−3j→+4k→\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k} . So, let AC→=3i→+j→−2k→\overrightarrow{AC}=3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k} and BD→=i→−3j→+4k→\overrightarrow{BD}=\overrightarrow{i}-3\overrightarrow{j}+4\overrightarrow{k} . For more clarity look at the figure given below:

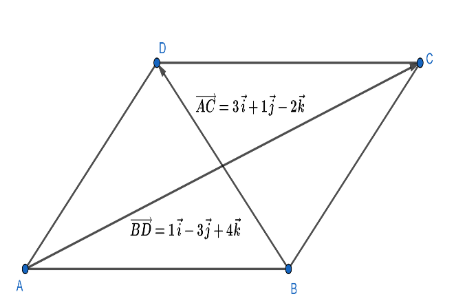
Now, to find the area of the given parallelogram we have to find the magnitude of the vector 12(AC→×BD→)\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right) . Then,
12(AC→×BD→)=12∣i→j→k→ 31−2 1−34 ∣\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=\dfrac{1}{2}\left| \begin{matrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\\ 3 & 1 & -2 \\\ 1 & -3 & 4 \\\ \end{matrix} \right|
Now, we will use the following formula of determinant to find the determinant value:
∣A∣=∣a11a12a13 a21a22a23 a31a32a33 ∣ ⇒∣A∣=a11(a22a33−a23a32)−a12(a21a33−a23a31)+a13(a21a32−a22a31) \begin{aligned} & \left| A \right|=\left| \begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \\\ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \\\ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \\\ \end{matrix} \right| \\\ & \Rightarrow \left| A \right|={{a}_{11}}\left( {{a}_{22}}{{a}_{33}}-{{a}_{23}}{{a}_{32}} \right)-{{a}_{12}}\left( {{a}_{21}}{{a}_{33}}-{{a}_{23}}{{a}_{31}} \right)+{{a}_{13}}\left( {{a}_{21}}{{a}_{32}}-{{a}_{22}}{{a}_{31}} \right) \\\ \end{aligned}

& \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=\dfrac{1}{2}\left| \begin{matrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\\ 3 & 1 & -2 \\\ 1 & -3 & 4 \\\ \end{matrix} \right| \\\ & \Rightarrow \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=\dfrac{1}{2}\left[ \left( 1\times 4-\left( -2 \right)\times \left( -3 \right) \right)\overrightarrow{i}-\left(3\times 4-(-2)\times 1 \right)\overrightarrow{j}+\left( -3\times 3-1\times 1 \right)\overrightarrow{k} \right] \\\ & \Rightarrow \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=\dfrac{1}{2}\left[ \left( 4-6 \right)\overrightarrow{i}-\left( 12+2 \right)\overrightarrow{j}+\left( -9-1 \right)\overrightarrow{k} \right] \\\ & \Rightarrow \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=\dfrac{1}{2}\left[ -2\overrightarrow{i}-14\overrightarrow{j}-10\overrightarrow{k} \right] \\\ & \Rightarrow \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=-\overrightarrow{i}-7\overrightarrow{j}-5\overrightarrow{k} \\\ \end{aligned}$$ Now, as we know that magnitude of the vector $x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$ is equal to $\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$ . Then, $$\begin{aligned} & \dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)=-\overrightarrow{i}-7\overrightarrow{j}-5\overrightarrow{k} \\\ & \Rightarrow \dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=\sqrt{{{1}^{2}}+{{7}^{2}}+{{5}^{2}}} \\\ & \Rightarrow \dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=\sqrt{1+49+25} \\\ & \Rightarrow \dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=\sqrt{75} \\\ & \Rightarrow \dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=\sqrt{25\times 3} \\\ & \Rightarrow \dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=5\sqrt{3} \\\ \end{aligned}$$ Now, as the magnitude of the vector $$\dfrac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{BD} \right|=5\sqrt{3}$$ . Thus, the area of the given parallelogram will be $5\sqrt{3}$ . Hence, (b) is the correct option. Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. And we should make use of the geometric meaning of $\dfrac{1}{2}\left( \overrightarrow{AC}\times \overrightarrow{BD} \right)$ to solve this question without any difficulty. Moreover, we should solve the cross product of the given vectors without any calculation mistake and select the correct answer.