Question

The area of the parallelogram formed by the lines $3x - 4y + 1 = 0$, $3x - 4y + 3 = 0$, $4x - 3y - 1 = 0$ and $4x - 3y - 2 = 0$ is
A. $\dfrac{1}{6}$sq units
B. $\dfrac{2}{7}$sq units
C. $\dfrac{3}{8}$sq units
D. None of the above

Answer 1

A parallelogram is formed by 4 lines. The area of this parallelogram is given by
$\Rightarrow$Area of parallelogram$= \left| {\dfrac{{\left( {{c_1} - {c_2}} \right)\left( {{d_1} - {d_2}} \right)}}{{{m_1} - {m_2}}}} \right|$
So, we need to convert the given equations to a standard slope intercept form that is $y = mx + c$ and then use this formula to find the area of the parallelogram.

Complete step by step answer:
In this question, we are given 4 equations of lines and we are supposed to find the area of the parallelogram formed by these lines.
First of all, let us see the concept of area of parallelogram when 4 equations of lines are given. So, let us draw a parallelogram first.

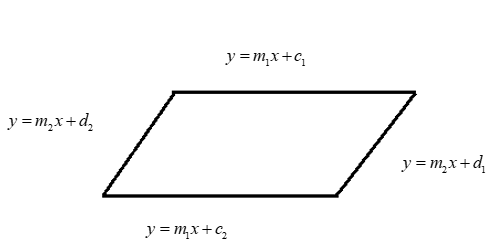
The above figure is of a parallelogram formed by 4 lines $y = {m_1}x + {c_1}$, $y = {m_1}x + {c_2}$, $y = {m_2}x + {d_1}$ and $y = {m_2}x + {d_2}$. Here, ${m_1}$ and ${m_2}$ are the slopes of the lines. Area of this parallelogram is given by
$\Rightarrow$Area of parallelogram$= \left| {\dfrac{{\left( {{c_1} - {c_2}} \right)\left( {{d_1} - {d_2}} \right)}}{{{m_1} - {m_2}}}} \right|$
Now, let us draw a parallelogram for our given equation

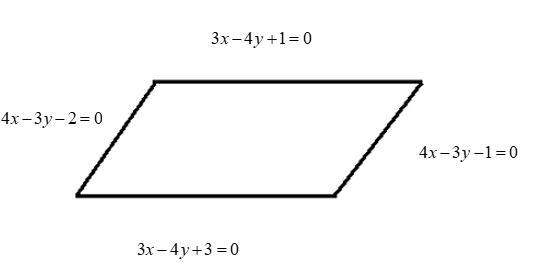
Now, we need to convert these equations in the form $y = mx + c$
Equation 1:
$\Rightarrow 3x - 4y + 1 = 0 \\\ \Rightarrow 4y = 3x + 1 \\\ \Rightarrow y = \dfrac{3}{4}x + \dfrac{1}{4} \\\$
Hence, ${m_1} = \dfrac{3}{4}$ and ${c_1} = \dfrac{1}{4}$
Equation 2:
$\Rightarrow 3x - 4y + 3 = 0 \\\ \Rightarrow 4y = 3x + 3 \\\ \Rightarrow y = \dfrac{3}{4}x + \dfrac{3}{4} \\\$
Hence, ${c_2} = \dfrac{3}{4}$
Equation 3:
$\Rightarrow 4x - 3y - 1 = 0 \\\ \Rightarrow 3y = 4x - 1 \\\ \Rightarrow y = \dfrac{4}{3}x - \dfrac{1}{3} \\\$
Hence, ${m_2} = \dfrac{4}{3}$ and ${d_1} = - \dfrac{1}{3}$
Equation 4:
$\Rightarrow 4x - 3y - 2 = 0 \\\ \Rightarrow 3y = 4x - 2 \\\ \Rightarrow y = \dfrac{4}{3}x - \dfrac{2}{3} \\\$
Hence, ${d_2} = - \dfrac{2}{3}$
Now, area of parallelogram is given by
$\Rightarrow$ Area of parallelogram$= \left| {\dfrac{{\left( {{c_1} - {c_2}} \right)\left( {{d_1} - {d_2}} \right)}}{{{m_1} - {m_2}}}} \right|$
Therefore,
$\Rightarrow$Area of parallelogram$= \left| {\dfrac{{\left( {\dfrac{1}{4} - \dfrac{3}{4}} \right)\left( { - \dfrac{1}{3} - \left( { - \dfrac{2}{3}} \right)} \right)}}{{\dfrac{3}{4} - \dfrac{4}{3}}}} \right|$
$= \left| {\dfrac{{\left( { - \dfrac{2}{4}} \right)\left( { - \dfrac{1}{3} + \dfrac{2}{3}} \right)}}{{\dfrac{{9 - 16}}{{12}}}}} \right| \\\ = \left| {\dfrac{{\left( { - \dfrac{1}{2}} \right)\left( {\dfrac{1}{3}} \right)}}{{\dfrac{{ - 7}}{{12}}}}} \right| \\\ = \left| {\dfrac{{\dfrac{1}{6}}}{{\dfrac{7}{{12}}}}} \right| \\\ = \left| {\dfrac{{1 \times 12}}{{6 \times 7}}} \right| \\\ = \left| {\dfrac{2}{7}} \right| \\\ = \dfrac{2}{7} \\\$
Hence, the area of parallelogram formed by the lines $3x - 4y + 1 = 0$, $3x - 4y + 3 = 0$, $4x - 3y - 1 = 0$ and $4x - 3y - 2 = 0$ is $\dfrac{2}{7}$sq units.
So, the correct answer is “Option B”.

Note: There are three points in this question that are very important.
The slope of parallel lines is always equal. Therefore, we can see that the slope of lines $3x - 4y + 1 = 0$, $3x - 4y + 3 = 0$ is equal to $\dfrac{3}{4}$.
Second point is that we have taken the formula of area of parallelogram in modulus as the value of area can never be negative.
Third most important point in this question is writing the unit while writing our final answer.