Question

The area of the parallelogram contained by the lines 4y-3x+1=0, 4y-3x-1=0, 3y-4x+1=0 and 3y-4x+2=0 is $\frac{p}{q}$, (in lowest form), then p + q is __.

Answer 1

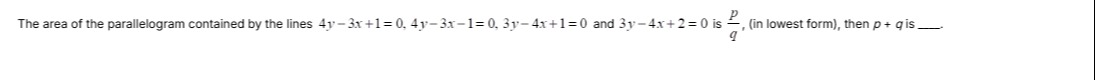
9

Answer 2

Solution:

We are given four lines:

$$\begin{aligned} L_1: &\quad 4y-3x+1=0,\\[5mm] L_2: &\quad 4y-3x-1=0,\\[5mm] L_3: &\quad 3y-4x+1=0,\\[5mm] L_4: &\quad 3y-4x+2=0. \end{aligned}$$

Step 1. Compute the distances between the parallel pairs using the distance formula for lines $Ax+By+C=0$:

$$d=\frac{|C_2-C_1|}{\sqrt{A^2+B^2}}.$$

For $L_1$ and $L_2$ (with coefficients $-3$ and $4$, so $\sqrt{9+16}=5$):

$$d_1=\frac{|(-1)-(+1)|}{5}=\frac{2}{5}.$$

For $L_3$ and $L_4$ (rewrite as $-4x+3y+C=0$, so the magnitude is again $5$):

$$d_2=\frac{|2-1|}{5}=\frac{1}{5}.$$

Step 2. Find the sine of the angle between the two families. The normals for the families are:

$$\begin{aligned} \mathbf{n_1}&=(-3,4) \quad (\text{from } L_1, L_2),\\[5mm] \mathbf{n_2}&=(-4,3) \quad (\text{from } L_3, L_4). \end{aligned}$$

Their dot product is:

$$\mathbf{n_1}\cdot\mathbf{n_2} = (-3)(-4)+4\cdot3=12+12=24.$$

The magnitudes are $|\mathbf{n_1}|=|\mathbf{n_2}|=5$. Thus,

$$\cos \theta = \frac{24}{5\cdot5}=\frac{24}{25}\quad\Rightarrow\quad \sin\theta=\sqrt{1-\left(\frac{24}{25}\right)^2}=\frac{7}{25}.$$

Step 3. The area $K$ of the parallelogram formed by these lines is:

$$K=\frac{d_1 \, d_2}{\sin\theta} = \frac{\left(\frac{2}{5}\right)\left(\frac{1}{5}\right)}{\frac{7}{25}}=\frac{\frac{2}{25}}{\frac{7}{25}}=\frac{2}{7}.$$

Here, $K=\frac{2}{7}$ with $p=2$ and $q=7$; therefore, $p+q = 2+7 = 9$.

---

Core Solution:

1. Distance between $4y-3x+1=0$ and $4y-3x-1=0$: $d_1=\frac{2}{5}$.

2. Distance between $3y-4x+1=0$ and $3y-4x+2=0$: $d_2=\frac{1}{5}$.

3. $\sin \theta=\frac{7}{25}$ where $\theta$ is the angle between the families.

4. Area $=\frac{d_1d_2}{\sin \theta}=\frac{2/25}{7/25}=\frac{2}{7}$ so $p+q=2+7=9$.