Question

The area of region bounded by $y = - 1$, $y = 2$,$x = {y^3}$ and $x = 0$ is
A. $\dfrac{{17}}{4}$ square units
B. $\dfrac{1}{4}$ square units
C. $4$ square units
D. None of these

Answer 1

Hint:- In this question use this concept that area under the curve region is calculated by doing integration between limits 'a' and 'b'.

Complete step-by-step solution -

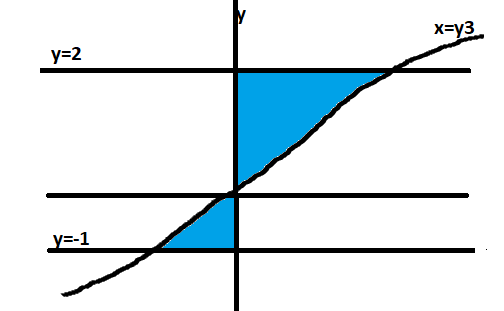
Area of bounded region = Area of above shaded curve region + Area of below shaded curve region
Area of above shaded curve region = Integration of$xdy$ from limit $0{\text{to2}}$
$= \int\limits_0^2 {xdy}$
value of $x = {y^3}$
$= \int\limits_0^2 {{y^3}dy} \\\ = \left[ {\dfrac{{{y^4}}}{4}} \right]_0^2 \\\ = 4{\text{uni}}{{\text{t}}^2} \\\$
Area of below shaded curve region = Integration of$xdy$ from limit $- 1{\text{to0}}$
$= \int\limits_{ - 1}^0 {xdy} \\\ = \int\limits_{ - 1}^0 {{y^3}dy} \\\ = \left[ {\dfrac{{{y^4}}}{4}} \right]_{ - 1}^0 \\\ = 0 - \left[ {\dfrac{1}{4}} \right] \\\ = - \dfrac{1}{4} \\\$
since area is in negative so we will take its mode so value will be $\dfrac{1}{4}$
Hence total area of bounded region = Area of above shaded region + Area of below shaded region
$= 4 + \dfrac{1}{4} \\\ = \dfrac{{16 + 1}}{4} \\\ = \dfrac{{17}}{4} \\\$
Hence the required area is $\dfrac{{17}}{4}$ units square.

Note:- As we know that total area of bounded region is equal to the area of above and below shaded curve region, hence we found the area of above shaded curve region by integration of$xdy$ from limit zero to two & area of below shaded curve region by integration of $xdy$ from limit minus one to zero after that we added both the values and got the required result.