Question

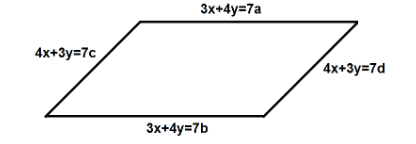
The area of parallelogram formed by the lines $3x + 4y = 7a$ , $3x + 4y = 7b$ , $4x + 3y = 7c$ and $4x + 3y = 7d$ is:
A. $\dfrac{{\left| {\left( {a - b} \right)\left( {c - d} \right)} \right|}}{7}$
B. $\left| {\left( {a - b} \right)\left( {c - d} \right)} \right|$
C. $\dfrac{{\left| {\left( {a - b} \right)\left( {c - d} \right)} \right|}}{{49}}$
D. $7\left| {\left( {a - b} \right)\left( {c - d} \right)} \right|$

Answer 1

Hint : Here, the four given lines form a parallelogram. For solving this problem, first we have to convert the equations of lines into the standard line form $y = mx + c$ . After that we can find the area of the parallelogram by using the formula or area of parallelogram when the lines forming that are given.
Formula used:
When a parallelogram is formed by four lines $y = {m_1}n + {c_1}$ , $y = {m_1}n + {c_2}$ , $y = {m_2}n + {d_1}$ and $y = {m_2}n + {d_2}$ , its area is given by:
$A = \left| {\dfrac{{\left( {{c_1} - {c_2}} \right)\left( {{d_1} - {d_2}} \right)}}{{{m_1} - {m_2}}}} \right|$

Complete step-by-step answer :

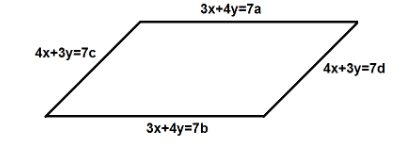
We are given that the parallelogram is formed by the lines $3x + 4y = 7a$ , $3x + 4y = 7b$ , $4x + 3y = 7c$ and $4x + 3y = 7d$ .
Our first step is to convert all the equations of lines into the standard line equation $y = mx + c$ .
Therefore, the first line $3x + 4y = 7a$ becomes $y = - \dfrac{3}{4}x + \dfrac{7}{4}a$
Comparing this equation with $y = {m_1}n + {c_1}$ , we get ${m_1} = - \dfrac{3}{4}$ and ${c_1} = \dfrac{7}{4}a$
The second line $3x + 4y = 7b$ becomes $y = - \dfrac{3}{4}x + \dfrac{7}{4}b$
Comparing this equation with $y = {m_1}n + {c_2}$ , we get ${m_1} = - \dfrac{3}{4}$ and ${c_2} = \dfrac{7}{4}b$
The third line $4x + 3y = 7c$ becomes $y = - \dfrac{4}{3}x + \dfrac{7}{3}c$
Comparing this equation with $y = {m_2}n + {d_1}$ , we get ${m_2} = - \dfrac{4}{3}$ and ${d_1} = \dfrac{7}{3}c$
The fourth line $4x + 3y = 7d$ becomes $y = - \dfrac{4}{3}x + \dfrac{7}{3}d$
Comparing this equation with $y = {m_2}n + {d_2}$ , we get ${m_2} = - \dfrac{4}{3}$ and ${d_2} = \dfrac{7}{3}d$
Now, we know that the area of the parallelogram is given by:
$A = \left| {\dfrac{{\left( {{c_1} - {c_2}} \right)\left( {{d_1} - {d_2}} \right)}}{{{m_1} - {m_2}}}} \right|$
We will now put the values of all the terms from the equations of given lines in the standard form, as we have determined.

$$\Rightarrow A = \left| {\dfrac{{\left( {\dfrac{7}{4}a - \dfrac{7}{4}b} \right)\left( {\dfrac{7}{3}c - \dfrac{7}{3}d} \right)}}{{ - \dfrac{3}{4} - \left( { - \dfrac{4}{3}} \right)}}} \right| \\\ \Rightarrow A = \left| {\dfrac{{\dfrac{7}{4}\left( {a - b} \right) \times \dfrac{7}{3}\left( {c - d} \right)}}{{ - \dfrac{3}{4} + \dfrac{4}{3}}}} \right| \\\ \Rightarrow A = \left| {\dfrac{{\dfrac{{49}}{{12}}\left( {a - b} \right)\left( {c - d} \right)}}{{\dfrac{{ - 9 + 16}}{{12}}}}} \right| \\\ \Rightarrow A = \left| {\dfrac{{\dfrac{{49}}{{12}}\left( {a - b} \right)\left( {c - d} \right)}}{{\dfrac{7}{{12}}}}} \right| \\\ \Rightarrow A = 7\left| {\left( {a - b} \right)\left( {c - d} \right)} \right| \\\$$

Thus, the area of the parallelogram formed by the lines $3x + 4y = 7a$ , $3x + 4y = 7b$ , $4x + 3y = 7c$ and $4x + 3y = 7d$ is $7\left| {\left( {a - b} \right)\left( {c - d} \right)} \right|$
So, the correct answer is “Option D”.

Note : The most important step to consider while solving this question is to convert the equations of lines into the standard forms in order to determine the terms required to find the area of the parallelogram. Here, the lines with the same slopes are the parallel sides of the parallelogram. Fore example, $3x + 4y = 7a$ and $3x + 4y = 7b$ have the same slope which is ${m_1} = - \dfrac{3}{4}$ , whereas the other two lines $4x + 3y = 7c$ and $4x + 3y = 7d$ have the same slope which is ${m_2} = - \dfrac{4}{3}$ . Therefore the parallelogram formed by these lines will be as shown in figure.