Question
Question: The area of \[\Delta ABC\] is \[32\] square cm. AD is median and E is the midpoint of AD. Find the a...
The area of ΔABC is 32 square cm. AD is median and E is the midpoint of AD. Find the area of ΔBED.
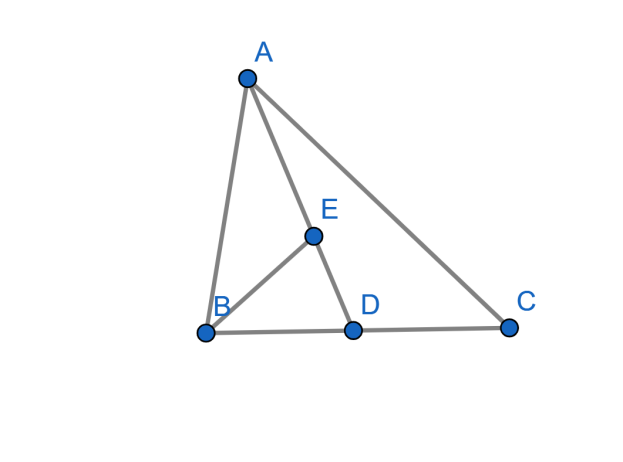
Solution
From the given question we have been asked to find the area of the triangle ΔBED where the area of triangle ΔABC is given. For solving this question we have to take the median in the triangle ΔABC using that we will use the property in similar triangles that is we bring the relation among the areas of the triangles inscribed in it and further solve the given question using basic mathematical operation like multiplication etc…so, the solution will be as follows.
Complete step by step solution:
Firstly, from the figure which is given we know that in ΔADB BE is the median line.
Which means the area of the triangle, ΔADB is equally separated or we can say that the median divides the given figure in equal parts.
So, we can say that,
⇒area(ΔBED)=area(ΔAEB)
From the question we are given that AD is the median of the triangle ΔABC. So, we can say that the area is equally divided or simply the area of the triangle ΔADB and ΔADCare equal.
So, we get,
⇒area(ΔBED)=area(ΔAEB)=21area(ΔABD)
So, we substitute the given area of ΔABC as 32 square cm.
We get the equation reduced as follows.
⇒area(ΔBED)=21(16)sqcm
⇒area(ΔBED)=8sqcm
Note: Students must be very careful in doing the calculations. Students should know the concept of triangles and median to triangle concepts.
For solving this question we use similar triangles concepts. We should know that area(ΔBED)=area(ΔAEB)=21area(ΔABD) to solve the question.
