Question
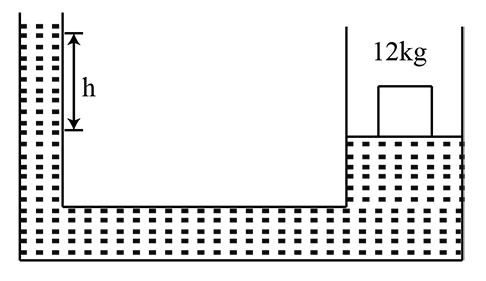
Question: The area of cross-section of the wider tube shown in figure is \[800c{m^2}\] . If a mass of \[12kg\]...
The area of cross-section of the wider tube shown in figure is 800cm2 . If a mass of 12kg is placed on the massless piston, the difference in heights h in the level of water in the two tubes is :
(A)10cm
(B)6cm
(C)15cm
(D)2cm
Solution
A piston is a disk or cylindrical part tightly fitting and moving within a cylinder, either to compress or move a fluid collected in the cylinder, as air or water, or to transform energy imparted by a fluid entering or expanding inside the cylinder, as compressed air, explosive gases, or steam, into a rectilinear motion usually transformed into rotary motion by means of a connecting rod.
Complete step by step solution:
Firstly, we need to understand what is the function of a Piston. In an engine, its purpose is to transfer force from expanding gas in the cylinder to the crankshaft via a piston rod or connecting rod. In a pump, the function is reversed and force is transferred from the crankshaft to the piston for the purpose of compressing or ejecting the fluid in the cylinder.
Given,
A=800cm3
m=12kg=12000gm
Here, the force on the piston is F=mg
Hence, we can say that the increase in the pressure on the liquid in the wider tube is
P=AF.......(1)
We also know that F=mg
So, we can write equation (1) as,
P=Amg
Since, h is the difference in the level of water in the two tubes,
P=hρg
h=ρgP
The above equation can also be written as,
h=Aρgmg=Aρm
Now, by putting the values, we get,
h=80012000.......(∵ρ=1)
h=15cm
Therefore, the correct answer is (C)15cm
Note:
It is important to note that this question needs to be solved in the CGS unit system. In fluid mechanics, the symbol ρ represents fluid density and the fluid density ρ for water is always 1cm3gm . But this value changes with the change in temperature or if some other substance is dissolved in the water.
