Question

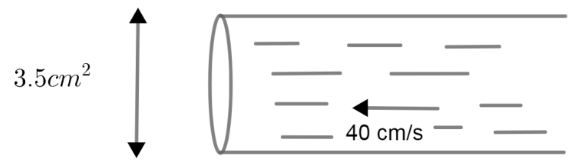
The area of cross-section of a pipe is ${\rm{3}}.{\rm{5}}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}$and water is flowing out of pipe at the rate of 40 cm/s. How much water is delivered by the pipe in one minute?

Answer 1

Hint: By using the rate given in the question. Find the amount of water coming from the pipe per minute. Now if you multiply this area of cross-section of the pipe then you will get the amount of water coming from the pipe per minute.

Complete step-by-step solution -
Given the area of cross-section of pipe in the question is:
$A = 3.5c{m^2}$ ……………….(1)
Rate is a differential value which says change of a thing with respect to the corresponding change of other things:
Given the value of rate in the question, assumed to be r:
$r = 40cm/s$
By the above value, we can say that the statement to be as:
40cm water is coming out per second.

The relation between a second and a minute is given by:
1 minute = 60 seconds
By dividing with 60 into both sides, we get it as
$\dfrac{{60}}{{60}}\text{seconds} = \dfrac{1}{{60}}\; \text{minute}$
By simplifying the above relation, we get the relation as:
$1{\rm{ second = }}\dfrac{1}{{60}}\; \text{minute}$
So, we have the statement given in the question as:
40 cm of water flows in each second.
By using the relation of the second, minute we can write:
40 cm water flow in $\dfrac{1}{{60}}\; \text{minute}.$
By adding the same statement 60 times, we can write:
$40 \times 60cm$ water flow in $\dfrac{1}{{60}} \times 60\; \text{minute}.$
By simplifying the above statement, we can say it as:
$40 \times 60cm$ water flow in 1 minute.
We need the amount of water flow per minute.
So, this amount multiplied by area will give volume of water flowing out:
Let the value required be w. By above, we get it as:
$w = r \times A$
From above r per minute has a value of $40 \times 60cm$.
By substituting this value and area give, we can write it as:
$w = \left( {40 \times 60cm} \right)\left( {3.5c{m^2}} \right)$
By simplifying the above equation, we can write it as:
$w = \left( {2400cm} \right) \times \left( {3.5c{m^2}} \right)$
By multiplying finally, we get the value of w as:
$w = 8400c{m^3}$. As we know$1{\rm{ litre = 1000c}}{{\rm{m}}^{\rm{3}}}$, we write
$w = \dfrac{{8400}}{{1000}}litre{\rm{ = 8}}{\rm{.4lts}}{\rm{.}}$
Therefore the volume of water coming out per minute is 8.4 liters.

Note: Be careful while calculating the rate. As some students divide by 60 instead of multiplying by 60. This may affect the whole answer. At last, the step also remembers, you must divide by 1000 not multiply. We don’t per minute as the rate is valued by per minute no need to mention it in w.