Question

The area of a loop of the curve $r = a\sin 3\theta$ is:
A. $\dfrac{{\pi {a^2}}}{2}$
B. $\dfrac{{\pi {a^2}}}{6}$
C. $\dfrac{{\pi {a^2}}}{8}$
D. $\dfrac{{\pi {a^2}}}{{12}}$

Answer 1

In this problem, first we need to find the upper and lower limits of the first loop of the curve. Then, apply the formula for the area under the curve in polar coordinates to obtain the area of the first loop.

Complete step-by-step answer:
The diagram of the curve $r = a\sin 3\theta$ is shown below.

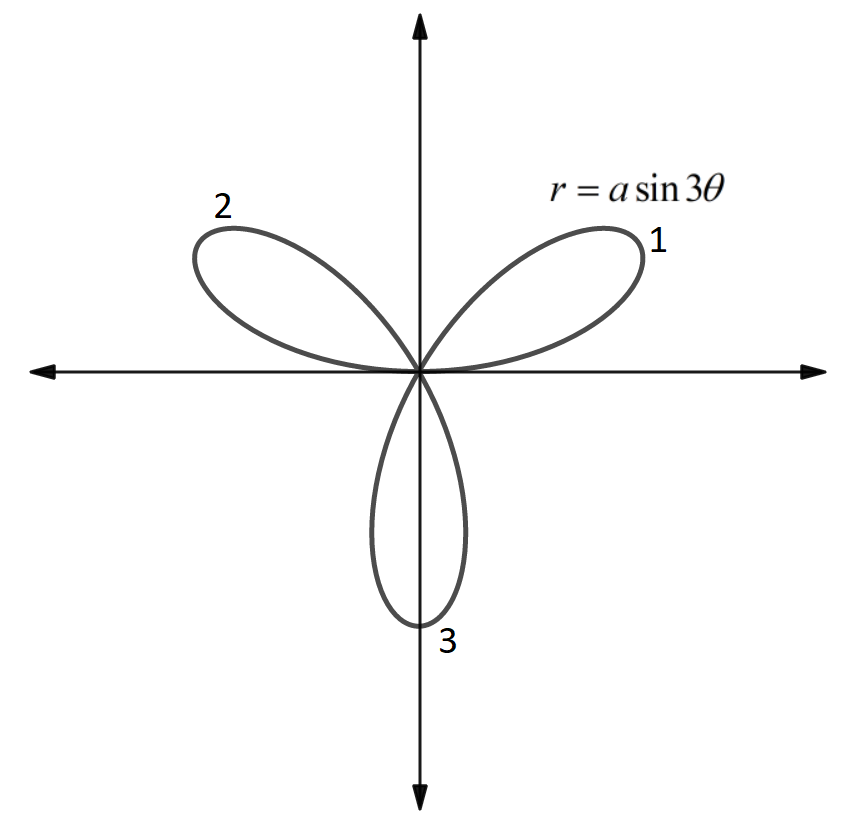
From the above figure, it can be observed that the curve$r = a\sin 3\theta$ consists of three loops.
Substitute 0 for $r$ in the equation of the curve $r = a\sin 3\theta$ to obtain the upper and lower limits of the loop.

$$\,\,\,\,\,\,0 = a\sin 3\theta \\\ \Rightarrow \sin 3\theta = 0 \\\ \Rightarrow 3\theta = 0\,\,{\text{or}}\,\,\pi \\\ \Rightarrow \theta = 0\,\,{\text{or}}\,\,\dfrac{\pi }{3} \\\$$

Here, 0 is the lower limits and $\dfrac{\pi }{3}$ is the upper limit of the first loop.
Now, the area $A$ of the first loop is calculated as follows:

$$\,\,\,\,\,\,A = \dfrac{1}{2}\int_0^{\dfrac{\pi }{3}} {{r^2}d\theta } \\\ \Rightarrow A = \dfrac{1}{2}\int_0^{\dfrac{\pi }{3}} {{a^2}{{\sin }^2}3\theta d\theta } \\\ \Rightarrow A = \dfrac{{{a^2}}}{2}\int_0^{\dfrac{\pi }{3}} {{{\sin }^2}3\theta d\theta } \\\ \Rightarrow A = \dfrac{{{a^2}}}{2}\int_0^{\dfrac{\pi }{3}} {\left( {\dfrac{{1 - \cos 6\theta }}{2}} \right)d\theta } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{{\sin }^2}\theta = \dfrac{{1 - \cos 2\theta }}{2}} \right) \\\$$

Further, solve the above integral as shown below.

$$\,\,\,\,\,\,\,A = \dfrac{{{a^2}}}{4}\int_0^{\dfrac{\pi }{3}} {\left( {1 - \cos 6\theta } \right)d\theta } \\\ \Rightarrow A = \dfrac{{{a^2}}}{4}\left[ {\theta - \dfrac{{\sin 6\theta }}{6}} \right]_0^{\dfrac{\pi }{3}} \\\ \Rightarrow A = \dfrac{{{a^2}}}{4}\left[ {\dfrac{\pi }{3} - \dfrac{{\sin 2\pi }}{6}} \right] \\\ \Rightarrow A = \dfrac{{{a^2}}}{4}\left[ {\dfrac{\pi }{3} - 0} \right] \\\ \Rightarrow A = \dfrac{{\pi {a^2}}}{{12}} \\\$$

Thus, the area of a loop of the curve $r = a\sin 3\theta$ is $\dfrac{{\pi {a^2}}}{{12}}$, hence, option (D) is correct answer.

Note: In this problem, there are three identical loops. The area of each loop is the same. While evaluating the integral, convert ${\sin ^2}3\theta$ into $\cos 6\theta$ using trigonometric identity.