Question
Question: The area of a circle inscribed in an equilateral triangle is \[154\text{ c}{{\text{m}}^{\text{2}}}\]...
The area of a circle inscribed in an equilateral triangle is 154 cm2. The side of the triangle is:
(a) 73
(b) 143
(c) 53
(d) 102
Solution
Hint: In this question, first of all, draw the diagram to get a clear idea about the question. Then divide the equilateral triangle into three parts and write the area of each part in terms of sides of the triangle and radius of the circle. Also, write the total area of the equilateral triangle, i.e. 43a2. Equate both of these to get the value of sides of the triangle.
Complete step-by-step answer:
Here, we are given that the area of the circle inscribed in an equilateral triangle is 154 cm2. We have to find the side of the triangle.
First of all, we know that the equilateral triangle is a triangle in which the length of all the sides is equal and each interior angle is of 60o.
Let us consider the condition given in question diagrammatically.
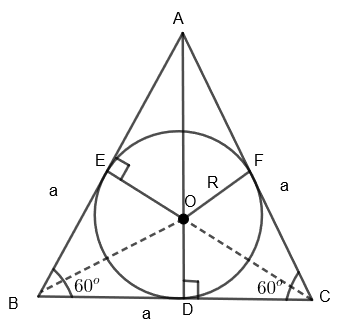
In the above diagram, ABC is an equilateral triangle with each side equal to ‘a’ and a circle is inscribed in it whose radius is ‘R’.
Here, we are given that area of the circle =154 cm2.
We know that the area of the circle =πR2
So, we get, πR2=154 cm2
By substituting π=722, we get,
722R2=154
Or, R2=227×154
By simplifying the above equation, we get,
R2=49
By taking square root on both the sides, we get,
R = 7 cm.
Now, we know that the area of the equilateral triangle, ΔABC = 43a2....(i)
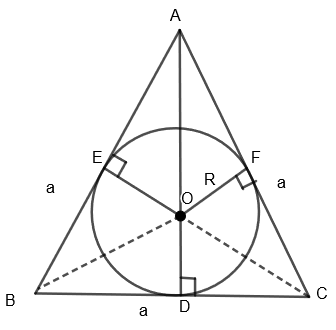
Here AB = AC = BC = a and OE = OF = OD = R
Also, we can say that area of the equilateral triangle
ΔABC = area of (ΔAOB+ΔAOC+ΔBOC)....(ii)
We know that the area of the triangle =\dfrac{1}{2}$$$$\times \left( \text{Base of the triangle} \right)\times \left( \text{Height of the triangle} \right)
Here, we can see that OE, OF, and OD are the height of the triangles ΔAOB, ΔAOC and ΔBOC. So, we get,
Area of ΔAOB=21AB×OE=21×a×R
Area of ΔAOC=21AC×OF=21×a×R
Area of ΔBOC=21BC×OD=21×a×R
By substituting these values in equation (ii), we get,
Area of equilateral ΔABC=21aR+21aR+21aR=23aR....(iii)
Now by equating equation (i) and (iii), we get,
43a2=23aR
By dividing 23a on both the sides, we get,
R=4.3a3a2.2=23a
We know that R = 7 cm.
By substituting the value of R, we get,
7=23a
By cross multiplying the above equation, we get
a=143 cm
So, we have got the side of the triangle as 143 cm.
Hence option (b) is the right answer.
Note:
In this question, we can see that a circle is inscribed in the triangle, which means this circle is incircle of the triangle. So students can directly remember that inradius of the equilateral triangle is 231 times the side of the triangle that is R=23a. Here, R is the inradius of the given incircle.
