Question

The area (in square units) bounded by the curve $y = \sqrt x$, $2y - x + 3 = 0$, X-axis and lying in the first quadrant is:
A. 36
B. 18
C. $\dfrac{{27}}{4}$
D. 9

Answer 1

To solve this question, we will use the concept of application of integral. We will find the area of bounded regions. The curve $y = \sqrt x$ represents a parabola with equation ${y^2} = 4ax$, Also find the intersection point of the curve and line for limits of integration.

Complete step-by-step answer :
Given that,
Curve, $y = \sqrt x$
Squaring both sides,
${y^2} = x$
This is a parabola.
Line = $2y - x + 3 = 0$ and X-axis and 1st quadrant.
Taking line, $2y - x + 3 = 0$
Let us find out its points.

x	0	3
y	$\dfrac{{ - 3}}{2}$	0

Points are (0, $\dfrac{{ - 3}}{2}$) and (3,0) and many more.
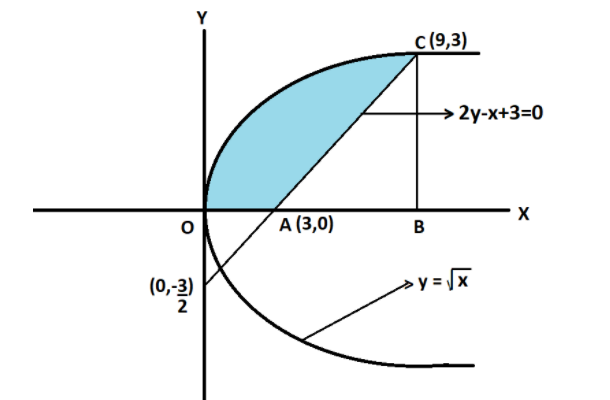
Now, we have to draw this curve and lines.
We have to find the area of OAC,
$\Rightarrow$ area of OAC = area of OABCO – area of $\vartriangle ABC$.
Here, we have to find the point C,
We can see that C is the intersection point of $y = \sqrt x$ and $2y - x + 3 = 0$
Putting $y = \sqrt x$ in $2y - x + 3 = 0$, we will get
$\Rightarrow 2\sqrt x - x + 3 = 0 \\\ \Rightarrow 2\sqrt x = x - 3 \\\$
Squaring both sides,
$\Rightarrow 4x = {\left( {x - 3} \right)^2} \\\ \Rightarrow 4x = {x^2} - 6x + 9 \\\ \Rightarrow {x^2} - 6x - 4x + 9 = 0 \\\ \Rightarrow {x^2} - 10x + 9 = 0 \\\ \Rightarrow {x^2} - 9x - x + 9 = 0 \\\ \Rightarrow x\left( {x - 9} \right) - 1\left( {x - 9} \right) = 0 \\\ \Rightarrow \left( {x - 1} \right)\left( {x - 9} \right) = 0 \\\$
Hence, we get x = 1 or 9.
Now, putting x = 9 in equation of line, we will get
$\Rightarrow 2y - 9 + 3 = 0 \\\ \Rightarrow 2y = 6 \\\ \Rightarrow y = 3 \\\$
Thus, the coordinates of point C will be (9,3).
Now,
$\Rightarrow$ area of OAC = area of OABCO – area of $\vartriangle ABC$.
$\Rightarrow$ area of OAC = $\int\limits_0^9 {\sqrt x dx} - \dfrac{1}{2}\left( 6 \right)\left( 3 \right)$
$\Rightarrow$ area of OAC = $\left[ {\dfrac{{{x^{\dfrac{1}{2} + 1}}}}{{^{\dfrac{1}{2} + 1}}}} \right]_0^9 - \dfrac{1}{2}\left( 6 \right)\left( 3 \right)$
$\Rightarrow$ area of OAC = $\left[ {\dfrac{{2{x^{\dfrac{3}{2}}}}}{3}} \right]_0^9 - 9$
$\Rightarrow$ area of OAC = $\left[ {\dfrac{2}{3}\left( {{9^{\dfrac{3}{2}}} - 0} \right)} \right] - 9$

$\Rightarrow$ area of OAC = $\left[ {\dfrac{2}{3}\left( {27} \right)} \right] - 9$
$\Rightarrow$ area of OAC = $18 - 9$
$\Rightarrow$ area of OAC = 9 square units.
Hence, the area bounded by the curve $y = \sqrt x$, $2y - x + 3 = 0$, X-axis and lying in the first quadrant is 9 square units.
Therefore, the correct answer is option (D).

Note : If the position of the curve under consideration is below the x-axis and since $f\left( x \right) < 0$ from x=a to x=b, the area bounded by the curve, x-axis and the coordinates x=a. x=b come out to be negative. But, it is only the numerical value of the area which is taken into consideration. Thus, if the area is negative, we take its absolute value.