Question

The area (in square unit) of the circle, which touches the lines $4x + 3y = 15$ and $4x + 3y = 5$ is $m\pi$. Find $m$.

Answer 1

First we will have the diameter, which is same as the perpendicular distance between two lines, $ax + by + c = 0$ and $ax + by + d = 0$ is$\dfrac{{\left| {c - d} \right|}}{{\sqrt {{a^2} + {b^2}} }}$ units. Then we will draw the diagram and then find the value of $a$, $b$, $c$, and $d$ in the formula. Then we will use the given conditions to find the required value.

Complete step-by-step answer:
We are given that the area (in square unit) of the circle, which touches the lines $4x + 3y = 15$ and $4x + 3y = 5$ is $m\pi$.

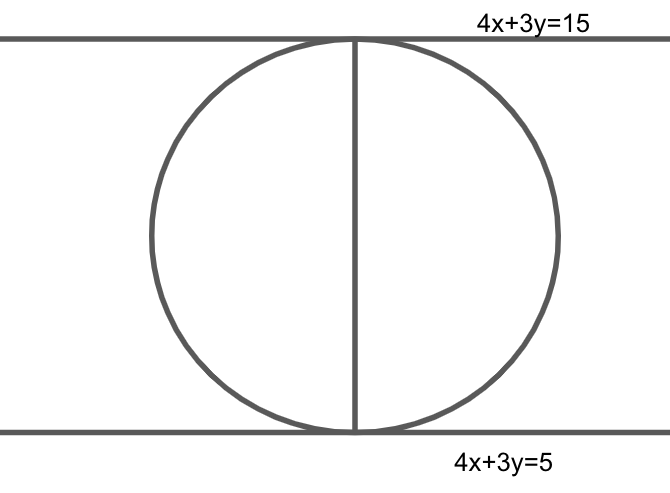
Rewriting the given equation, we get
$4x + 3y - 15 = 0{\text{ ......eq.(1)}}$
$4x + 3y - 5 = 0{\text{ ......eq.(2)}}$
Since it is clear that the given lines are parallel, so we will have the diameter, which is same as the perpendicular distance between two lines, $ax + by + c = 0$ and $ax + by + d = 0$ is$\dfrac{{\left| {c - d} \right|}}{{\sqrt {{a^2} + {b^2}} }}$ units.
Finding the value of $a$, $b$, $c$, and $d$ from the equations (1) and (2), we get
$a = 4$
$b = 3$
$c = - 15$
$d = - 5$
Substituting the value of $a$, $b$, $c$, and $d$ in the formula of perpendicular distance between two lines, we get

$$\Rightarrow \dfrac{{\left| { - 15 - \left( { - 5} \right)} \right|}}{{\sqrt {{4^2} + {3^2}} }} \\\ \Rightarrow \dfrac{{\left| { - 15 + 5} \right|}}{{\sqrt {16 + 9} }} \\\ \Rightarrow \dfrac{{\left| { - 10} \right|}}{{\sqrt {25} }} \\\ \Rightarrow \dfrac{{10}}{5} \\\ \Rightarrow 2{\text{ units}} \\\$$

So, the diameter is 2 units.
Dividing the above diameter by 2 to find the radius of the circle, we get
$\Rightarrow \dfrac{2}{2} = 1{\text{ units}}$
Using the formula of area of circle is ,$\pi {r^2}$ where $r$ is the radius, we get

$$\Rightarrow \pi {\left( 1 \right)^2} \\\ \Rightarrow \pi \left( 1 \right) \\\ \Rightarrow \pi {\text{ units}} \\\$$

So, we have according to the problem is $m\pi = \pi$.
Dividing the above equation by $\pi$ on both sides, we get

$$\Rightarrow \dfrac{{m\pi }}{\pi } = \dfrac{\pi }{\pi } \\\ \Rightarrow m = 1 \\\$$

Therefore, the required value is 1.

Note: We know that the perpendicular distance formula of the lines is used and we see that the perpendicular distance between two lines, $ax + by + c = 0$ and $ax + by + d = 0$ is$\dfrac{{\left| {c - d} \right|}}{{\sqrt {{a^2} + {b^2}} }}$. Also, we are supposed to avoid calculations. We have to find the radius, do not solve using the diameter or else the answer will be wrong. Diagrams will help in better understanding.