Solveeit Logo
Login

Question

Question: The area (in sq. units) of the smaller potion enclosed between the curves, \({{x}^{2}}+{{y}^{2}}=4\)...

The area (in sq. units) of the smaller potion enclosed between the curves, x2+y2=4{{x}^{2}}+{{y}^{2}}=4 and y2=3x{{y}^{2}}=3x, is.
(a) 13+4π3\dfrac{1}{\sqrt{3}}+\dfrac{4\pi }{3}
(b) 123+π3\dfrac{1}{2\sqrt{3}}+\dfrac{\pi }{3}
(c) 123+2π3\dfrac{1}{2\sqrt{3}}+\dfrac{2\pi }{3}
(d) 13+2π3\dfrac{1}{\sqrt{3}}+\dfrac{2\pi }{3}

Explanation

Solution

To understand the question better, we will first draw the figure of the curves x2+y2=4{{x}^{2}}+{{y}^{2}}=4 and y2=3x{{y}^{2}}=3x. Then we will solve the equations of the curves to get the coordinates of the points at which they intersect. Then, we find the area under the individual curves. Then we will add these areas.

Complete step by step answer:
The first curve given to us is x2+y2=4{{x}^{2}}+{{y}^{2}}=4.
As we can see, the curve is a circle with centre at the origin and the radius as 2 units.
The second curve given to us is y2=3x{{y}^{2}}=3x.
This curve is a parabola with the vertex at the origin and focus at (3, 0).
The diagram of the curves are as follows:

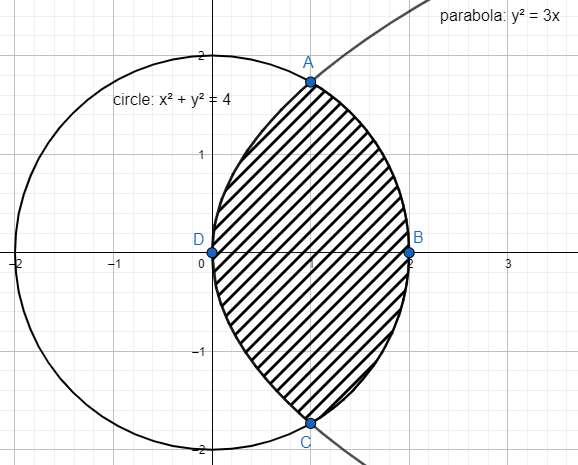
We have to find the area of the curves between ABCD (region with hatching lines).
Coordinates of point D is (0, 0) and that of point B is (2, 0)
As we can see, the area is divided into two parts. If we find the area of one of the parts, we can multiply that area by 2 to get the total area.
To find point A, we have to solve the equation of the circle x2+y2=4{{x}^{2}}+{{y}^{2}}=4 and the parabola y2=3x{{y}^{2}}=3x.
We will substitute y2=3x{{y}^{2}}=3x into x2+y2=4{{x}^{2}}+{{y}^{2}}=4
⇒x2+3x=4 ⇒x2+3x−4=0 \begin{aligned} & \Rightarrow {{x}^{2}}+3x=4 \\\ & \Rightarrow {{x}^{2}}+3x-4=0 \\\ \end{aligned}
This is a quadratic equation for x. We will solve this quadratic equation by factorisation method.
We will split the middle terms as 4x and ─ x.
⇒x2+4x−x−4=0 ⇒x(x+4)−1(x+4)=0 ⇒(x+4)(x−1)=0 \begin{aligned} & \Rightarrow {{x}^{2}}+4x-x-4=0 \\\ & \Rightarrow x\left( x+4 \right)-1\left( x+4 \right)=0 \\\ & \Rightarrow \left( x+4 \right)\left( x-1 \right)=0 \\\ \end{aligned}
Thus x = ─ 4 and x = 1. But we can see that y2=3x{{y}^{2}}=3x doesn’t exist for negative values.
Therefore x – coordinate of point A is 1.
We will integrate the curve y=3xy=\sqrt{3x} from 0 to 1 and y=4−x2y=\sqrt{4-{{x}^{2}}} from 1 to 2 and add them up. This will give us the area of the upper part.

& \Rightarrow \dfrac{1}{2}A=\int\limits_{0}^{1}{\sqrt{3x}}dx+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}}dx \\\ & \Rightarrow \dfrac{1}{2}A=\sqrt{3}\left( \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right)_{0}^{1}+\left( \dfrac{x}{2}\sqrt{4-{{x}^{2}}}+2{{\sin }^{-1}}\dfrac{x}{2} \right)_{1}^{2} \\\ & \Rightarrow \dfrac{1}{2}A=\sqrt{3}\left( \dfrac{2}{3} \right)+\left\\{ 2\dfrac{\pi }{2}-\left( \dfrac{\sqrt{3}}{2}+\dfrac{\pi }{3} \right) \right\\} \\\ & \Rightarrow \dfrac{1}{2}A=\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}}{2}+\dfrac{2\pi }{3} \\\ & \Rightarrow \dfrac{1}{2}A=\dfrac{1}{2\sqrt{3}}+\dfrac{2\pi }{3} \\\ & \Rightarrow A=\dfrac{1}{\sqrt{3}}+\dfrac{4\pi }{3} \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** It is always advised to draw figures whenever possible. It might give insights to the question and reveal information, which might be overseen without the figures.