Question

The area (in sq. units) of the region \left\\{ x\in \mathbb{R}:x\ge 0,y\ge 0,y\ge x-2\text{ and }y\le \sqrt{x} \right\\}, is:

Answer 1

In this type of question we have to use the concept of finding the area of the region bounded by two curves. First we have to draw the given curves so that we can identify the required region and then we can find out the area of the region by using integration and after evaluating the integration we can obtain the required area.

Complete step-by-step solution:
Now we have to find the area in sq. units of the region \left\\{ x\in \mathbb{R}:x\ge 0,y\ge 0,y\ge x-2\text{ and }y\le \sqrt{x} \right\\}. First we will draw the given curves to identify the required region as follows:

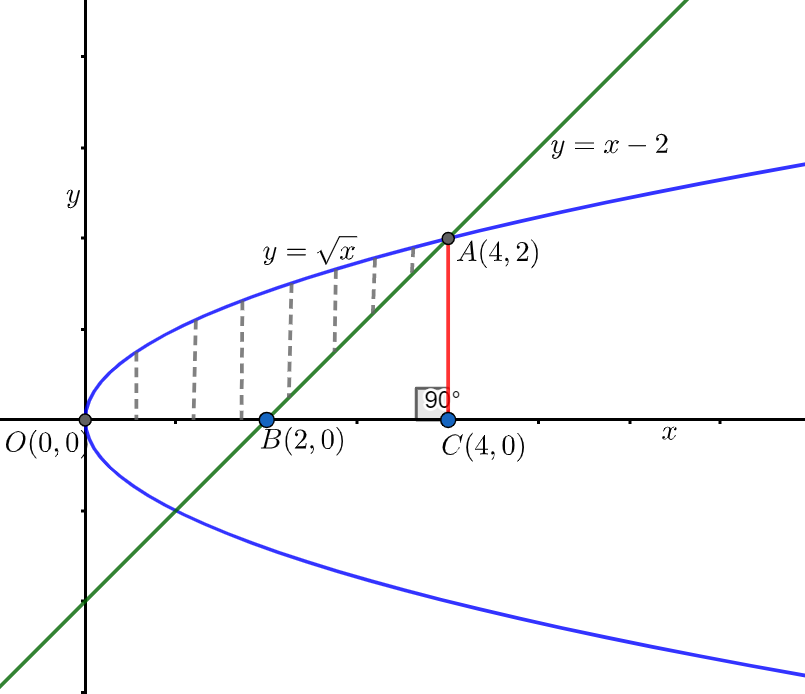
As we have given that, the region is bounded by $x\ge 0,y\ge 0,y\ge x-2\text{ and }y\le \sqrt{x}$ hence we can say that the required region is bounded by positive x-axis, positive y-axis, above the line $y=x-2$and below the curve $y=\sqrt{x}$ i.e. ${{y}^{2}}=x$.
Now to find out the area of the required region let us consider, find out the points of intersection first.
As we have given that, $y=\sqrt{x}$ and $y=x-2$, we can write,
$\Rightarrow \sqrt{x}=x-2$
On squaring both sides and further simplifying we get,

& \Rightarrow {{\left( \sqrt{x} \right)}^{2}}={{\left( x-2 \right)}^{2}} \\\ & \Rightarrow x={{x}^{2}}-4x+4 \\\ & \Rightarrow {{x}^{2}}-5x+4=0 \\\ & \Rightarrow \left( x-4 \right)\left( x-1 \right)=0 \\\ & \Rightarrow x=4,x=1 \\\ \end{aligned}$$ $$\Rightarrow y=2,y=-1$$ Hence, the points of intersection are $$\left( 4,2 \right)\And \left( 1,-1 \right)$$. But as the region is bounded by positive x-axis and positive y-axis, we have to consider only one point of interaction i.e. $$\left( 4,2 \right)$$. Therefore we can obtain the area of the required region by subtracting the area of the triangle ABC from the area of positive $$y=\sqrt{x}$$ up to $$x=4$$. $$\Rightarrow \text{Area of the region = }\int\limits_{0}^{4}{\sqrt{x}dx-\text{ Area of the triangle ABC}}\text{ }$$ As the triangle ABC is right angled triangle with height and base equal to 2 units, we can write, $$\Rightarrow \text{Area of the region = }\int\limits_{0}^{4}{\sqrt{x}dx-\text{ }\dfrac{1}{2}\times 2\times 2}$$ Now, as we know that, $$\sqrt{x}$$ can be written as, $${{x}^{\dfrac{1}{2}}}$$ we get, $$\Rightarrow \text{Area of the region = }\int\limits_{0}^{4}{{{x}^{\dfrac{1}{2}}}dx-\text{ }2}$$ By evaluating the definite integral and on simplification we get, $$\begin{aligned} & \Rightarrow \text{Area of the region = }\left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{0}^{4}-2 \\\ & \Rightarrow \text{Area of the region = }\dfrac{2}{3}\left( {{4}^{\dfrac{3}{2}}} \right)-2 \\\ & \Rightarrow \text{Area of the region = }\dfrac{2\times 8}{3}-2 \\\ & \Rightarrow \text{Area of the region = }\dfrac{16}{3}-2 \\\ & \Rightarrow \text{Area of the region = }\dfrac{10}{3}\text{ sq}\text{. units} \\\ \end{aligned}$$ **Hence, The area of the region $\left\\{ x\in \mathbb{R}:x\ge 0,y\ge 0,y\ge x-2\text{ and }y\le \sqrt{x} \right\\}$, is $$\dfrac{10}{3}\text{ sq}\text{. units}$$.** **Note:** In this type of question students have to note that they have to draw the given curves first; it will help them to identify the region and hence the corresponding limits. Students have to take care in evaluating the integration as the power of x is in terms of fraction. Also students have to take care in simplifying the power of 4 as again it is in the form of a fraction.