Question

The area (in sq. units) of the region bounded by the curves $y = {2^x}$ and $y = |x + 1|$, in the first quadrant is :
A. $\dfrac{3}{2} - \dfrac{1}{{{{\log }_e}2}}$
B. $\dfrac{1}{2}$
C. ${\log _e}2 + \dfrac{3}{2}$
D. $\dfrac{3}{2}$

Answer 1

We will first construct the figure as the area of the region bounded by the given curves. We have to find the area of the region in the first quadrant only. As the curve $y = |x + 1|$ lies above and the other curve $y = {2^x}$ lies below so we will subtract the upper from the lower curve and find the limits to determine the area of the bounded region.

Complete step by step answer:

We will first construct both the given curves in the first quadrant and find the limits under which the area needs to be found.

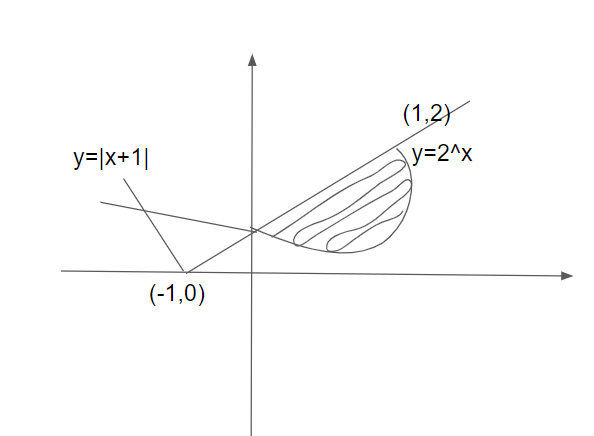
From the figure, we can see that the curve $y = {2^x}$ lies below and the curve $y = |x + 1|$ lies above the shaded region.
We have to find the area of the shaded region which is lying between the interval $\left[ {0,1} \right]$ and we will subtract the curve bounded below from the curve bounded above.
Thus, we get the integral as:

$$\Rightarrow I = \int\limits_0^1 {\left( {\left( {x + 1} \right) - {2^x}} \right)} dx \\\ \Rightarrow I = \left[ {\dfrac{{{x^2}}}{2} + x - \dfrac{{{2^x}}}{{{{\log }_e}2}}} \right]_0^1 \\\$$

Since, we have used the basic integration to integrate $\int {xdx = \dfrac{{{x^2}}}{2}}$ and $\int {{2^x} = \dfrac{{{2^x}}}{{{{\log }_e}2}}}$.
Now, we will apply the limits on the obtained integral value by substituting 1 in place of $x$ and then 0 in place of $x$,
Thus, we get,

$$\Rightarrow I = \left[ {\dfrac{{{1^2}}}{2} + 1 - \dfrac{{{2^1}}}{{{{\log }_e}2}}} \right] - \left[ {0 + 0 - \dfrac{1}{{{{\log }_e}2}}} \right] \\\ \Rightarrow I = \dfrac{3}{2} - \dfrac{1}{{{{\log }_e}2}} \\\$$

Thus, we get the area of the bounded region as $I = \dfrac{3}{2} - \dfrac{1}{{{{\log }_e}2}}$.
Hence, option A is correct.

Note: We have integrated the term ${2^x} = \dfrac{{{2^x}}}{{{{\log }_e}2}}$ using the basic knowledge of integration. Constructing the figure in such questions will make the solution easier as the area of the bounded region will be easily determined by subtracting the upper region from the lower region. Also, the limit can also be found from the figure. Basic integration formulas or methods should be in mind to solve such questions. While solving the integration, do it correctly and apply the limits after finding the integration of the functions.