Question

The area (in sq. units) of the parallelogram whose diagonals are along the vectors $8\hat{i}-6\hat{j}$ and $3\hat{i}+4\hat{j}-12\hat{k}$ is.
(a) 65
(b) 20
(c) 26
(d) 52

Answer 1

To understand the question better, we will first draw a diagram. It is given that the diagonals are along two vectors. Thus, their lengths will be equal to the magnitudes of the respective vectors. The dot product of two vectors a and b is defined as $a.b=\left| a \right|\left| b \right|\cos \theta$, $\left| a \right|$ is the magnitude of vector a, $\left| b \right|$ is the magnitude of vector b and $\theta$ is the angle between the two vectors. Once we get the angle between the vectors, we can find the height of one of the two equal triangles formed by the diagonal of the parallelogram. With the height, we will find the area of the triangle whose base will be one of the diagonals and hence, the length of the base will be equal to the length of that diagonal. This area of the triangle will be exactly half that the area of the parallelogram.

Complete step by step answer:
Let ABCD be the parallelogram with diagonals $8\hat{i}-6\hat{j}$ and $3\hat{i}+4\hat{j}-12\hat{k}$.
We will also construct perpendicular CE on diagonal BD and perpendicular AF on the same diagonal BD.
The diagram of the parallelogram is as follows:

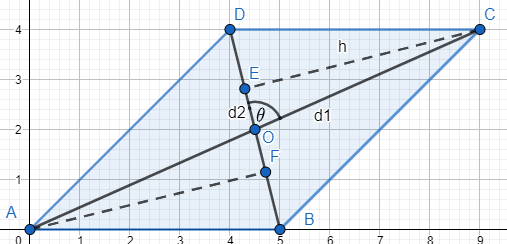
We can see that the parallelogram is divided into two equal triangles BCD and BAD. If we find the area of one of the triangles, we can double it to find the area of the parallelogram.
In triangle BCD, CE acts as the height of the triangle. The length of CO is half the length of AC.
Now, the diagonals are ${{d}_{1}}=3\hat{i}+4\hat{j}-12\hat{k}$ and ${{d}_{2}}=8\hat{i}-6\hat{j}$.
Therefore, we will find the lengths of the diagonals.
$\begin{aligned} & \Rightarrow \left| {{d}_{1}} \right|=\sqrt{{{3}^{2}}+{{4}^{2}}+{{12}^{2}}} \\\ & \Rightarrow \left| {{d}_{1}} \right|=\sqrt{169} \\\ & \Rightarrow \left| {{d}_{1}} \right|=13 \\\ & \Rightarrow \left| {{d}_{2}} \right|=\sqrt{{{8}^{2}}+{{6}^{2}}} \\\ & \Rightarrow \left| {{d}_{2}} \right|=\sqrt{100} \\\ & \Rightarrow \left| {{d}_{2}} \right|=10 \\\ \end{aligned}$
Thus, BD is 10 units and AC is 13 units.
Therefore, CO will be $\dfrac{13}{2}$ units.
Now, to find $\theta$, we will use the relation of the dot product of two vectors.
Dot product of any two vectors ${{r}_{1}}=a\hat{i}+b\hat{j}+c\hat{k}$ and ${{r}_{2}}=p\hat{i}+q\hat{j}+r\hat{k}$ is represented as ${{r}_{1}}.{{r}_{2}}$ and its value is ${{r}_{1}}.{{r}_{2}}=ap+bq+cr$. It is a scalar quantity. Moreover, it is defined as ${{r}_{1}}.{{r}_{2}}=\left| {{r}_{1}} \right|\left| {{r}_{2}} \right|\cos \theta$, where $\theta$ is the angle between two vectors.
$\begin{aligned} & \Rightarrow {{d}_{1}}.{{d}_{2}}=\left| {{d}_{1}} \right|\left| {{d}_{2}} \right|\cos \theta \\\ & \Rightarrow \cos \theta =\dfrac{3\left( 8 \right)-4\left( 6 \right)}{10\left( 13 \right)} \\\ & \Rightarrow \cos \theta =0 \\\ & \Rightarrow \theta =\dfrac{\pi }{2} \\\ \end{aligned}$
If the angle between the diagonals is $\dfrac{\pi }{2}$, this means CO and CE are the same line and half of the diagonal AC.
Thus, the area of the triangle BCD is $\dfrac{1}{2}\left( BD \right)\left( CO \right)$.
$\begin{aligned} & \Rightarrow A=\dfrac{1}{2}\left( 10 \right)\left( \dfrac{13}{2} \right) \\\ & \Rightarrow A=\dfrac{130}{4} \\\ & \Rightarrow A=\dfrac{65}{2} \\\ \end{aligned}$
Area of the parallelogram is twice that of the triangle.
Thus, the area of parallelogram is 65 sq units.

So, the correct answer is “Option A”.

Note: The figure thus formed with diagonals of different length at right angle will be rectangle. Area of a triangle can be directly remembered as $\dfrac{1}{2}{{d}_{1}}{{d}_{2}}$.