Solveeit Logo
Login

Question

Question: The area (in sq. units) bounded by the parabola \(y={{x}^{2}}-1\), the tangent at the point (2,3) to...

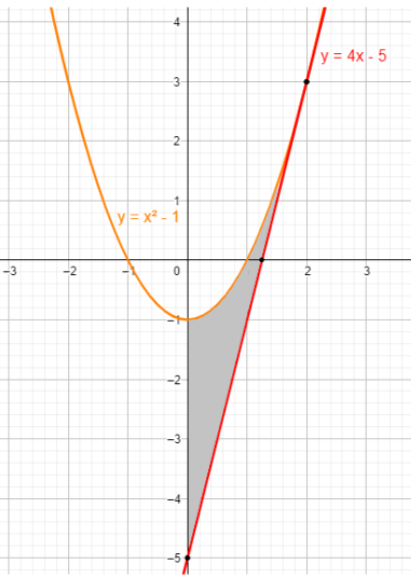
The area (in sq. units) bounded by the parabola y=x2−1y={{x}^{2}}-1, the tangent at the point (2,3) to it and the y-axis is
(A)143 (B)563 (C)83 (D)323 \begin{aligned} & \left( A \right)\dfrac{14}{3} \\\ & \left( B \right)\dfrac{56}{3} \\\ & \left( C \right)\dfrac{8}{3} \\\ & \left( D \right)\dfrac{32}{3} \\\ \end{aligned}

Explanation

Solution

We start solving this question by finding the slope of the tangent to the curve at (2,3) by differentiating the curve and substituting the point (2,3) and we use the formula ddxxn=n×xn−1\dfrac{d}{dx}{{x}^{n}}=n\times {{x}^{n-1}}. From the obtained slope and point we find the equation of line using the formula, (y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right). Then we plot the graph of the curve and the tangent. Then we divide the region into two parts and find their areas by integrating them using the formula ∫xndx=xn+1n+1\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1} and add them to find the total area.

Complete step-by-step solution:
Given that a tangent is drawn to the parabola y=x2−1y={{x}^{2}}-1 at point (2,3). So, let us find the equation of the tangent to the curve.
To find the slope of the tangent, let us differentiate the equation with respective to x.
dydx=ddx(x2−1) dydx=2x \begin{aligned} & \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}}-1 \right) \\\ & \dfrac{dy}{dx}=2x \\\ \end{aligned}
Then at point (2,3), slope of tangent is,
dydx=2x]x=2=4\dfrac{dy}{dx}={{\left. 2x \right]}_{x=2}}=4
So, slope of the tangent is equal to 4.
Now let us consider the formula for line equation from slope and point.
(y−y1)=m(x−x1)\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)
So, using the above formula we get,

⇒(y−3)=4(x−2) ⇒y−3=4x−8 ⇒y=4x−5 \begin{aligned} & \Rightarrow \left( y-3 \right)=4\left( x-2 \right) \\\ & \Rightarrow y-3=4x-8 \\\ & \Rightarrow y=4x-5 \\\ \end{aligned}
So, equation of the tangent at (2,3) is y=4x−5y=4x-5.
Now, let us plot the graph for the given curves.

Now, let us divide our required region into two parts, above x-axis and below x-axis. So, let us find the point where the line intersects x-axis. On x-axis y=0. So,
⇒4x−5=0 ⇒4x=5 ⇒x=54 \begin{aligned} & \Rightarrow 4x-5=0 \\\ & \Rightarrow 4x=5 \\\ & \Rightarrow x=\dfrac{5}{4} \\\ \end{aligned}
Let us use the formula for finding the area between two curves f(x)f\left( x \right) and g(x)g\left( x \right) and x-axis between x=a and x=b is
∫ab(f(x)−g(x))dx\int\limits_{a}^{b}{\left( f\left( x \right)-g\left( x \right) \right)dx}
Using the above formula, for the region below x-axis, we get
⇒∫054((4x−5)−(x2−1))dx ⇒∫054(−x2+4x−4)dx ⇒[−x33+2x2−4x]054 ⇒[(−(54)33+2(54)2−4(54))−(−033+2(0)2−4(0))] ⇒[(−125643+2(2516)−5)−(0)] ⇒(−125192+258−5) ⇒(475192−5) ⇒(475192−5) ⇒−485192 \begin{aligned} & \Rightarrow \int\limits_{0}^{\dfrac{5}{4}}{\left( \left( 4x-5 \right)-\left( {{x}^{2}}-1 \right) \right)dx} \\\ & \Rightarrow \int\limits_{0}^{\dfrac{5}{4}}{\left( -{{x}^{2}}+4x-4 \right)dx} \\\ & \Rightarrow \left[ -\dfrac{{{x}^{3}}}{3}+2{{x}^{2}}-4x \right]_{0}^{\dfrac{5}{4}} \\\ & \Rightarrow \left[ \left( -\dfrac{{{\left( \dfrac{5}{4} \right)}^{3}}}{3}+2{{\left( \dfrac{5}{4} \right)}^{2}}-4\left( \dfrac{5}{4} \right) \right)-\left( -\dfrac{{{0}^{3}}}{3}+2{{\left( 0 \right)}^{2}}-4\left( 0 \right) \right) \right] \\\ & \Rightarrow \left[ \left( -\dfrac{\dfrac{125}{64}}{3}+2\left( \dfrac{25}{16} \right)-5 \right)-\left( 0 \right) \right] \\\ & \Rightarrow \left( -\dfrac{125}{192}+\dfrac{25}{8}-5 \right) \\\ & \Rightarrow \left( \dfrac{475}{192}-5 \right) \\\ & \Rightarrow \left( \dfrac{475}{192}-5 \right) \\\ & \Rightarrow -\dfrac{485}{192} \\\ \end{aligned}
As the area is positive quantity, we take the area of first part as 485192\dfrac{485}{192}…………(1)
Now, let us find the area of second part that is above x-axis.
⇒∫542((x2−1)−(4x−5))dx ⇒∫542(x2−4x+4)dx ⇒[x33−2x2+4x]542 ⇒[(233−2(2)2+4(2))−((54)33−2(54)2+4(54))] ⇒[(83−8+8)−(125643−2(2516)+5)] ⇒(83)−(125192−258+5) ⇒(83)−(−475192+5) ⇒83−485192 ⇒27192.................(2) \begin{aligned} & \Rightarrow \int\limits_{\dfrac{5}{4}}^{2}{\left( \left( {{x}^{2}}-1 \right)-\left( 4x-5 \right) \right)dx} \\\ & \Rightarrow \int\limits_{\dfrac{5}{4}}^{2}{\left( {{x}^{2}}-4x+4 \right)dx} \\\ & \Rightarrow \left[ \dfrac{{{x}^{3}}}{3}-2{{x}^{2}}+4x \right]_{\dfrac{5}{4}}^{2} \\\ & \Rightarrow \left[ \left( \dfrac{{{2}^{3}}}{3}-2{{\left( 2 \right)}^{2}}+4\left( 2 \right) \right)-\left( \dfrac{{{\left( \dfrac{5}{4} \right)}^{3}}}{3}-2{{\left( \dfrac{5}{4} \right)}^{2}}+4\left( \dfrac{5}{4} \right) \right) \right] \\\ & \Rightarrow \left[ \left( \dfrac{8}{3}-8+8 \right)-\left( \dfrac{\dfrac{125}{64}}{3}-2\left( \dfrac{25}{16} \right)+5 \right) \right] \\\ & \Rightarrow \left( \dfrac{8}{3} \right)-\left( \dfrac{125}{192}-\dfrac{25}{8}+5 \right) \\\ & \Rightarrow \left( \dfrac{8}{3} \right)-\left( -\dfrac{475}{192}+5 \right) \\\ & \Rightarrow \dfrac{8}{3}-\dfrac{485}{192} \\\ & \Rightarrow \dfrac{27}{192}.................\left( 2 \right) \\\ \end{aligned}
Then the total area is sum of both areas. So, adding the obtained areas in equation (1) and (2) we get,
⇒485192+27192 ⇒512192 ⇒83 \begin{aligned} & \Rightarrow \dfrac{485}{192}+\dfrac{27}{192} \\\ & \Rightarrow \dfrac{512}{192} \\\ & \Rightarrow \dfrac{8}{3} \\\ \end{aligned}
So, total area of the region bounded by given curves is 83\dfrac{8}{3} square units.
Hence answer is Option C.

Note: There is a possibility of making a mistake while solving this question by not taking the modulus of −485192-\dfrac{485}{192}, and leaving it as it is. Then they add it with 27192\dfrac{27}{192} to find the total area. But it is wrong. The first part of the region is below the x-axis that is the reason we get the area as negative. So, we need to take the modulus of the area of the first part −485192-\dfrac{485}{192}, and add it to 27192\dfrac{27}{192}.