Question

The area (equal to A) and angle $\theta$ of a triangle is given, if the side opposite to the given angle is minimum in length, then the length of other two sides are:
A) $\sqrt {\dfrac{{2A}}{{\sin \theta }}} {\text{ and }}\sqrt {\dfrac{{3A}}{{\sin \theta }}}$
B) $\sqrt {\dfrac{{2A}}{{\sin \theta }}} {\text{ and }}\sqrt {\dfrac{{2A}}{{\sin \theta }}}$
C) $\sqrt {\dfrac{{4A}}{{\sin \theta }}} {\text{ and }}\sqrt {\dfrac{{2A}}{{\sin \theta }}}$
D) $\sqrt {\dfrac{{6A}}{{\sin \theta }}} {\text{ and }}\sqrt {\dfrac{{6A}}{{\sin \theta }}}$

Answer 1

When the two sides a and b of a triangle and the angle $\theta$ between them is given (SAS property), then the area of the triangle could be found by using the formula:
$Area = \dfrac{1}{2}ab\operatorname{Sin} \theta$
Apply this formula for the two sides two be found. Since, the area and angle of the triangle is already given, from the above formula we can find the value of the product of the two unknown sides. Check for all the options, and see which of them satisfy the condition for the product of two sides found from above.

Complete step by step solution:
Let us take a triangle ABC, and let the $\angle ABC = \theta$.
It is given that the side opposite to the angle $\theta$is shortest in length, hence the angle $\theta$ will be the smallest angle of the triangle. Because we know that the angle opposite to the largest side is always largest and the angle opposite to the shortest side is always the smallest angle in the triangle.

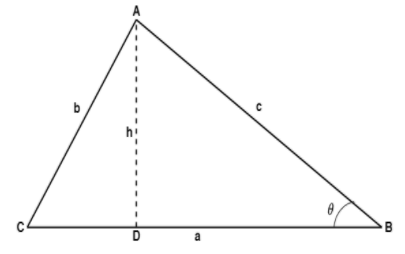
Now, let us take the height of the triangle to be h. i.e. AD = h.
Now, in Triangle ABD taking sine of the $\angle ABD$, we get:
$\operatorname{Sin} \theta = \dfrac{{AD}}{{AB}}{\text{ }}\left[ {\because \sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}} \right]$
$\Rightarrow \sin \theta = \dfrac{h}{c} \\\ \Rightarrow h = c \cdot \sin \theta - - - - - - - - - - - - - - - - - - [1] \\\$
Area of a triangle is given by:
$\dfrac{1}{2} \times base \times height$
Here, in the triangle ABC it is given that its area is equal to A, where base is ‘a’ and height is h.
$\Rightarrow A = \dfrac{1}{2} \times a \times h \\\ \Rightarrow A = \dfrac{1}{2} \times a \times c \times \sin \theta \\\ \Rightarrow A = \dfrac{1}{2}ac\sin \theta \\\$
Now, after rearrangement we get:
$ac = \dfrac{{2A}}{{\sin \theta }}$
It means that the product of the two sides is equal to $\dfrac{{2A}}{{\sin \theta }}$.
The only option which satisfies the above condition is option B.
Therefore, the length of the two sides is:
$a = c = \sqrt {\dfrac{{2A}}{{\operatorname{Sin} \theta }}}$

Since, both the sides are equal, hence the given triangle is an isosceles triangle.

Note:
If three sides of a triangle are given i.e. a, b and c respectively then the area of the triangle can be found by heron’s formula:
$Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$
Where, s is the semi-perimeter of the triangle given by:
$s = \dfrac{{a + b + c}}{2}$