Question

The area enclosed by the pair of lines $xy = 0$ , the line $x - 4 = 0$ and $y + 5 = 0$ is
$\left( 1 \right){\text{ 20 sq}}{\text{.units}}$
$\left( 2 \right){\text{ 10 sq}}{\text{.units}}$
$\left( 3 \right){\text{ }}\dfrac{5}{4}{\text{ sq}}{\text{.units}}$
$\left( 4 \right){\text{ 0 sq}}{\text{.units}}$

Answer 1

Hint : First use the given equations of lines and find the values of coordinate and then plot the graph by using these values. Then after plotting we will observe that the area which is enclosed by the given lines is of rectangular shape. Therefore we have to find the area of the enclosed area by using the formula of area of rectangle. The formula is Area $=$ length $\times$ breadth

Complete step-by-step answer :
We have to use given equations of line to make a graph. The given equations of lines are $xy = 0$ , the line $x - 4 = 0$ and $y + 5 = 0$
So now first we will solve the equation $xy = 0$ .On solving this equation we have
$\Rightarrow x = 0$ and $y = 0{\text{ }}$ ---------- (i)
Now we will solve the equation $x - 4 = 0$ .In this equation by shifting $4$ to the right hand side we get
$\Rightarrow x = 4$ ---------- (ii)
Similarly we will now solve the equation $y + 5 = 0$ .On shifting $5$ to the right hand side we get
$\Rightarrow y = - 5$ ---------- (iii)
Therefore by using equations (i) , (ii) and (iii) the below given graph will be make

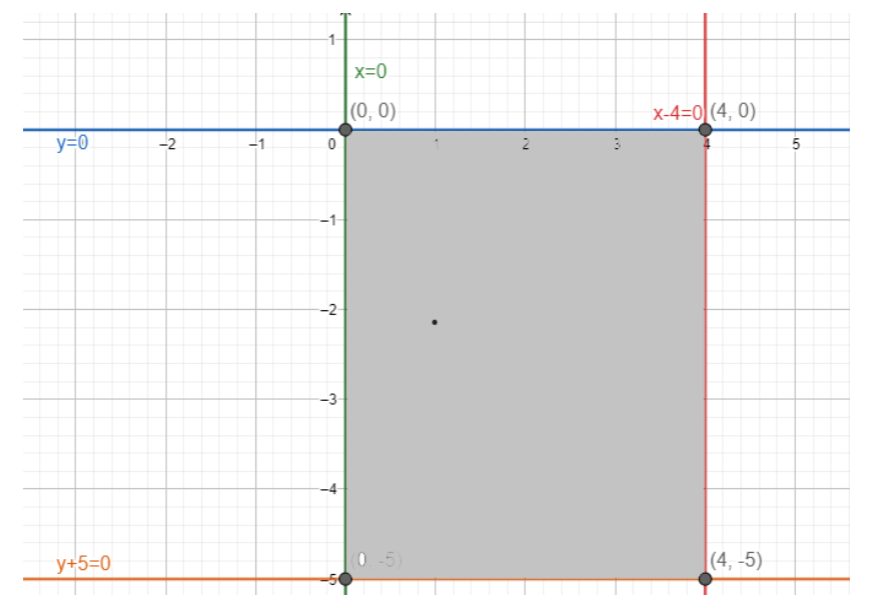
Now we have to find the area of the grey coloured region in the graph as shown below. We observe that the area of which we have to find the area has a rectangular shape. And we know that the area of any rectangle is calculated once its length and breadth (width) are known. By multiplying length and breadth the rectangle’s area will be obtained in a square unit dimension. The formula to find area of a rectangle is given below
Area of rectangle (A) $=$ length (l) $\times$ breadth (b)
The longest side of a rectangle is known as the length of the rectangle and the shortest side of a rectangle is known as the breadth or width of a rectangle. Therefore by observing the graph we can say that the length of the rectangular shaped region is $5$ and $4$ .
So, the area enclosed by the pair of lines $xy = 0$ , the line $x - 4 = 0$ and $y + 5 = 0$ is
Area $=$ length $\times$ breadth
$\Rightarrow 5 \times 4$
$\Rightarrow 20{\text{ sq}}{\text{.units}}$
Hence, the correct option is $\left( 1 \right){\text{ 20 sq}}{\text{.units}}$
So, the correct answer is “Option 1”.

Note : Keep in mind that length is the longest side of the rectangle and breadth/width is the shortest side of the rectangle. Keep in mind the formula to calculate the area of a rectangle. Remember that for areas we use square units. Carefully plot the graph by using the given equations.