Question

The area enclosed by the curves x² = y, y = x + 2 and x-axis is –

• A. $\frac { 5 } { 6 }$
• B. $\frac { 5 } { 4 }$
• C. $\frac { 5 } { 2 }$
• D. None of these

Answer 1

Answer: (A)

$\frac { 5 } { 6 }$

Answer 2

Intersection of x² = y and y = x + 2 is x² = x + 2

̃ x² – x – 2 = 0 ̃ (x – 2) (x + 1) = 0

̃x = – 1, x = 2 ̃ y = 1, y = 4

̃ A (–1, 1), B(2, 4)

Required area = A = (A₁ + A₂),

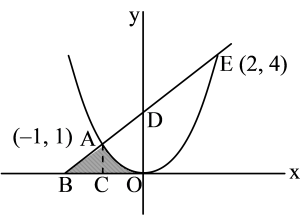
where A₁ = Area of

DABC =$\frac { 1 } { 2 }$AC × BC =$\frac { 1 } { 2 }$ (1) (1) =$\frac { 1 } { 2 }$

as OB = –2, CO = –1,

Area = A₂ = $\left| \int _ { - 1 } ^ { 0 } y d x \right|$ = $\left| \int _ { - 1 } ^ { 0 } x ^ { 2 } d x \right|$ = $\frac { 1 } { 3 }$

By (1), A = $\frac { 1 } { 2 }$ + $\frac { 1 } { 3 }$ = $\frac { 5 } { 6 }$