Question

The area enclosed by the curve $y = {x^2}$, $y = {x^3}$, $x = 0$ and $x = p$, where $p > 1$, is $\dfrac{1}{6}$. Then $p$ equals
A. $\dfrac{4}{3}$
B. $2$
C. $\dfrac{8}{3}$
D. $\dfrac{{16}}{3}$

Answer 1

Hint: Here, we will graph the given curves and then find the area of the enclosed area by taking the integration of the difference of the lower curve from the upper curve w.r.t. $x$–axis in the obtained interval. Then, we will find the area by adding the obtained integrations.

Complete step-by-step solution:
Given that the area enclosed by the curve is $\dfrac{1}{6}$.

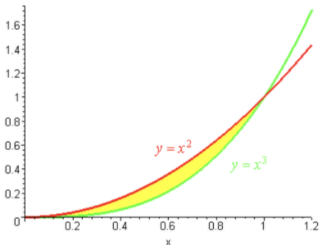
We first note that the curves intersect each other at the points $\left( {0,0} \right)$ and $\left( {1,1} \right)$.

Since ${x^2} > {x^3}$ inside this interval and ${x^2} < {x^3}$ outside this interval, we will find the area of the curve.

First, we will find the integration of the area enclosed from $x = 0$ to $x = 1$.

$${I_1} = \int\limits_{x = 0}^{x = 1} {\left( {{x^2} - {x^3}} \right)dx} \\\ = \left[ {\dfrac{{{x^3}}}{3} - \dfrac{{{x^4}}}{4}} \right]_{x = 0}^{x = 1} \\\ = \dfrac{1}{3} - \dfrac{1}{4} - 0 \\\ = \dfrac{{4 - 3}}{{12}} \\\ = \dfrac{1}{{12}} \\\$$

Now, we will find the integration of the area enclosed from $x = 1$ to $x = p$.

$${I_2} = \int\limits_{x = 1}^{x = p} {\left( {{x^3} - {x^2}} \right)dx} \\\ = \left[ {\dfrac{{{x^4}}}{4} - \dfrac{{{x^3}}}{3}} \right]_{x = 1}^{x = p} \\\ = \dfrac{{{p^4}}}{4} - \dfrac{{{p^3}}}{3} - \left( {\dfrac{1}{3} - \dfrac{1}{4}} \right) \\\ = \dfrac{{{p^4}}}{4} - \dfrac{{{p^3}}}{3} - \dfrac{1}{4} + \dfrac{1}{3} \\\ = \dfrac{{3{p^4} - 4{p^3} - 3 + 4}}{{12}} \\\ = \dfrac{{3{p^4} - 4{p^3} + 1}}{{12}} \\\$$

Adding ${I_1}$ and ${I_2}$, we get

$${I_1} + {I_2} = \dfrac{1}{{12}} + \dfrac{{3{p^4} - 4{p^3} + 1}}{{12}} \\\ = \dfrac{{3{p^4} - 4{p^3} + 2}}{{12}} \\\$$

Since we know that the area enclosed by the curve $y = {x^2}$, $y = {x^3}$, $x = 0$ and $x = p$, where $p > 1$, is $\dfrac{1}{6}$.

Taking the above integration equals to $\dfrac{1}{6}$, we get

$$\Rightarrow \dfrac{{3{p^4} - 4{p^3} + 2}}{{12}} = \dfrac{1}{6} \\\ \Rightarrow 3{p^4} - 4{p^3} + 2 = 2 \\\ \Rightarrow 3{p^4} - 4{p^3} = 0 \\\ \Rightarrow {p^3}\left( {3p - 4} \right) = 0 \\\$$

$\Rightarrow {p^3} = 0$ or $\Rightarrow 3p - 4 = 0$
$\Rightarrow p = 0$ or $\Rightarrow p = \dfrac{4}{3}$

Thus, the value of $p$ is either 0 or $\dfrac{4}{3}$ but p can’t be 0 as $p > 1$. So $p = \dfrac{4}{3}$ is correct.
Hence, the option A is correct.

Note: In this question, we are supposed to make the graph properly to avoid any miscalculation and subtract the lower curve from the upper curve to find the area enclosed between two curves.. Also, we will write the values of the obtained integration properly.