Question
Question: The area enclosed by $C_1$: y = Inx and $C_2$: y = $tan^{-1}$(x - 1) between the vertical lines x = ...
The area enclosed by C1: y = Inx and C2: y = tan−1(x - 1) between the vertical lines x = 1 and x = 2 (in square units) is equal to
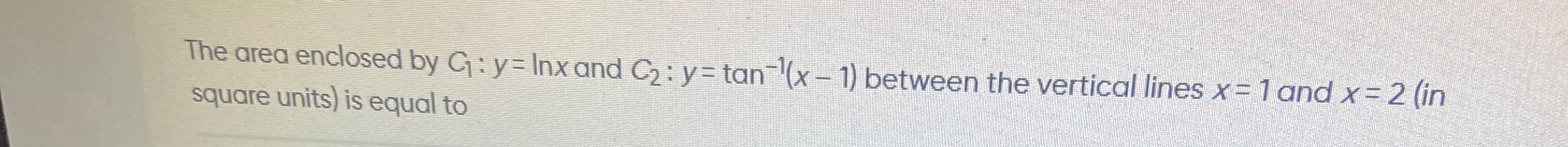
1+4π−25ln2
Solution
To find the area enclosed by the curves C1: y = ln x and C2: y = tan⁻¹(x - 1) between x = 1 and x = 2, we first need to determine which curve is above the other in the given interval.
-
Analyze the functions at the boundaries:
- At x = 1:
- For C1: y = ln(1) = 0.
- For C2: y = tan⁻¹(1 - 1) = tan⁻¹(0) = 0. Both curves pass through the point (1, 0).
- At x = 2:
- For C1: y = ln(2) ≈ 0.693.
- For C2: y = tan⁻¹(2 - 1) = tan⁻¹(1) = π/4 ≈ 0.785. Since π/4 > ln(2), at x = 2, C2 is above C1.
- At x = 1:
-
Determine which function is greater in the interval (1, 2): Let's consider the function f(x) = tan⁻¹(x - 1) - ln x. We want to find the sign of f(x) for x ∈ (1, 2). We know f(1) = 0. Let's find the derivative f'(x): f′(x)=dxd(tan−1(x−1))−dxd(lnx) f′(x)=1+(x−1)21−x1 f′(x)=x(1+(x−1)2)x−(1+(x−1)2) f′(x)=x(1+(x−1)2)x−(1+x2−2x+1) f′(x)=x(1+(x−1)2)x−x2+2x−2 f′(x)=x(1+(x−1)2)−x2+3x−2 f′(x)=x(1+(x−1)2)−(x2−3x+2) f′(x)=x(1+(x−1)2)−(x−1)(x−2) For x ∈ (1, 2):
- (x - 1) > 0
- (x - 2) < 0
- So, (x - 1)(x - 2) < 0.
- Therefore, -(x - 1)(x - 2) > 0.
- The denominator x(1 + (x - 1)²) is positive for x ∈ (1, 2). Thus, f'(x) > 0 for x ∈ (1, 2). Since f(1) = 0 and f(x) is increasing in (1, 2), it implies f(x) > 0 for x ∈ (1, 2). Therefore, tan⁻¹(x - 1) > ln x for x ∈ (1, 2). The area is given by the integral of the upper curve minus the lower curve: Area = ∫12(tan−1(x−1)−lnx)dx Area = ∫12tan−1(x−1)dx−∫12lnxdx
-
Evaluate ∫tan−1(x−1)dx: Let u = x - 1, so du = dx. The integral becomes ∫tan−1(u)du. Using integration by parts, ∫vdw=vw−∫wdv: Let v = tan⁻¹(u) and dw = du. Then dv = 1+u21du and w = u. ∫tan−1(u)du=utan−1(u)−∫1+u2udu For the second integral, let t = 1 + u², so dt = 2u du, which means u du = 21dt. ∫1+u2udu=∫2t1dt=21ln∣t∣=21ln(1+u2). So, ∫tan−1(u)du=utan−1(u)−21ln(1+u2). Substituting back u = x - 1: ∫tan−1(x−1)dx=(x−1)tan−1(x−1)−21ln(1+(x−1)2). Evaluating the definite integral from 1 to 2: [(2−1)tan−1(2−1)−21ln(1+(2−1)2)]−[(1−1)tan−1(1−1)−21ln(1+(1−1)2)] =[1⋅tan−1(1)−21ln(1+1)]−[0⋅tan−1(0)−21ln(1+0)] =[4π−21ln2]−[0−0] =4π−21ln2.
-
Evaluate ∫lnxdx: Using integration by parts: Let v = ln x and dw = dx. Then dv = x1dx and w = x. ∫lnxdx=xlnx−∫x⋅x1dx=xlnx−∫1dx=xlnx−x. Evaluating the definite integral from 1 to 2: [2ln2−2]−[1ln1−1] =[2ln2−2]−[0−1] =2ln2−2+1 =2ln2−1.
-
Calculate the total area: Area = (4π−21ln2)−(2ln2−1) Area = 4π−21ln2−2ln2+1 Area = 4π+1−(21+2)ln2 Area = 4π+1−(21+4)ln2 Area = 1+4π−25ln2.
The final answer is 1+4π−25ln2.
