Question

The area enclosed between the curve $y={{\log }_{e}}\left( x+e \right)$ and the coordinate axes is:
A) 3
B) 4
C) 1
D) 2

Answer 1

Here we have to find the area enclosed by the given curve and the coordinate axes. For that, we will trace the graph for the given curve and then we will find the points where the curve has cut the x and y axes. Then, we will find the area by integrating the given curve between the proper ranges.

Complete step by step solution:
The given curve is $y={{\log }_{e}}\left( x+e \right)$
First we will draw the curve on the coordinate axes.
At $x=0;y=1$
At $x=1-e;y=0$
We have got the points where the curve will cut the x-axis and y-axis. We will draw the curve using these points.

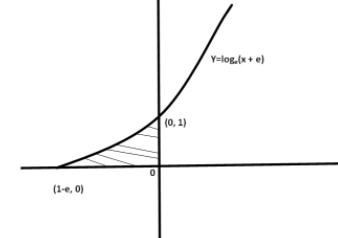
Now, we will calculate the shaded area by integrating it from $x=1-e$ to $x=0$
Area of the shaded region $=\int\limits_{1-e}^{0}{{{\log }_{e}}\left( x+e \right)}dx$
We will integrate by substitution method.
Let $x+e=t$
Differentiating both sides with respect to x, we get
$dx=dt$
At $x=1-e;t=1\text{ }\\!\\!\And\\!\\!\text{ at }x=0;t=e$
Therefore,
Area of the shaded region $=\int\limits_{1}^{e}{{{\log }_{e}}\left( t \right)}dt$
Now, we will integrate it.
Area of the shaded region $=\left[ t\log {{t}_{e}}-t \right]_{1}^{e}$
On simplifying it further, we get
Area of the shaded region $=\left[ e\log {{e}_{e}}-e-0-1 \right]$
Now, will put the value of here

Area of the shaded region $=\left[ e-e-0-1 \right]$ {As$\log {{e}_{e}}=1$ }
Now, we will subtract the similar terms.
Area of the shaded region $=1\text{sq}\text{.unit}$
Therefore,
Area enclosed between the curve $y={{\log }_{e}}\left( x+e \right)$ and the coordinate axes is 1sq.unit.

Thus, the correct option is C.

Note:
The important terms that we need to know are:-

1. An integration of any function f(x) is a method of finding a function h(x) whose derivative i.e. $\dfrac{dh(x)}{dx}$ is equal to the given function f(x).
2. A curve is defined as a line which is drawn smoothly in a plane and which doesn’t bend or turn anywhere in a plane.