Question

The area enclosed between the curve $y={{\log }_{e}}\left( x+e \right)$ and the coordinate axes is
(A) $4\text{ sq units}$
(B) $\text{3 sq units}$
(C) $\text{2 sq units}$
(D) $\text{1 sq unit}$

Answer 1

Hint: Try to find where the curve cuts the $x$ axis. First try to make a rough sketch. Then find the area under the curve using integral.

First, let’s try visualising the function given to us.
So, first of all let’s try plotting the curve considering various values,
Note that at $x=0,y=1$, at $x=-e+1,y=0$ and at $x=-e,y=-\infty$
Use above observations to plot the graph of $y={{\log }_{e}}\left( x+e \right)$.

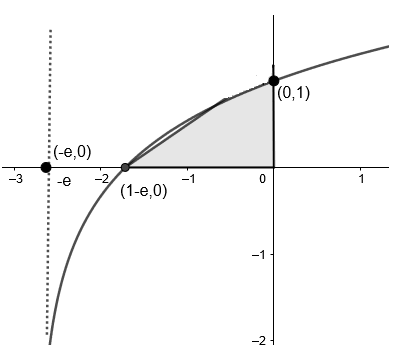
The shaded region is the required area.
Hence, we can now find the area by integrating the function from $x=1-e$ to $x=0$.
Now, to find the area enclosed by the figure, we can easily integrate in the interval $x\in (1-e,0)$, since in this interval, the position of the curves relative to each other and the $x$ axis remains the same.
The formula of finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
So the required area under the curve is,
$\text{Area}=\int\limits_{1-e}^{0}{{{\log }_{e}}\left( x+e \right)dx}$
Put $x+e=u$
$\Rightarrow dx=du$ as the derivation of $e$ is zero.
The integral can be written as
$Area=\int{{{\log }_{e}}\left( u \right)du}$
We will skip limits for now.
Use integration by parts i.e., $\int{fg'=fg-\int{f'g}}$, in the above expression $f={{\log }_{e}}u,g=u$, so it can be written as
$\Rightarrow \text{Area}=u{{\log }_{e}}u-\int{\left( \dfrac{d}{x}\left( {{\log }_{e}}u \right) \right)(u).du}$
Now we know differentiation of ${{\log }_{e}}x$ is $\dfrac{1}{x}$ , so the above equation becomes,

& \Rightarrow \text{Area}=u{{\log }_{e}}u-\int{\dfrac{1}{u}(u).du} \\\ & \Rightarrow \text{Area}=u{{\log }_{e}}u-\int{1.du} \\\ \end{aligned}$$ On integrating, we get $$\Rightarrow \text{Area}=\left[ u{{\log }_{e}}u-u \right]$$ Substituting back the value of $u$ and adding the limits , we get $$\Rightarrow \text{Area}=\left[ \left( x+e \right){{\log }_{e}}\left( x+e \right)-\left( x+e \right) \right]_{1-e}^{0}$$ Now applying the limits, we get $$\begin{aligned} & \Rightarrow \text{Area}=\left[ \left( 0+e \right){{\log }_{e}}\left( 0+e \right)-\left( 0+e \right) \right]-\left[ \left( 1-e+e \right){{\log }_{e}}\left( 1-e+e \right)-\left( 1-e+e \right) \right] \\\ & \Rightarrow \text{Area}=\left[ e{{\log }_{e}}\left( e \right)-e \right]-\left[ (1){{\log }_{e}}\left( 1 \right)-1 \right] \\\ \end{aligned}$$ We know, ${{\log }_{e}}e=1,{{\log }_{e}}1=0$ , so the above equation can be written as $$\begin{aligned} & \Rightarrow \text{Area}=\left[ e(1)-e \right]-\left[ (1)(0)-1 \right] \\\ & \Rightarrow \text{Area}=0-\left[ -1 \right]=1 \\\ \end{aligned}$$ Therefore the area under the curve is $1$ sq. units. Hence the correct answer is option (D). Answer is option (D) Note: Another alternate method is by integrating over the $y$ axis rather than the $x$ axis, i.e. finding out the area by integrating using $dy$ instead of $dx$. To do this however, you need to express each of the three lines as a function of $y$, rather than expressing them in terms of $x$, and you need to visualise which curve more to the right relative to the $y$ axis. The curve lying more to the right will be treated like the upper curve, and hence, we can find the area out in that way as well. But this will be complicated. Another possibility of mistake is that while using integration by parts, students might not change the upper and lower limit appropriately as per substitution.