Question

The area covered by a transmitting antenna of height 50 m is
A. $320\pi k{{m}^{2}}$
B. $1440\pi k{{m}^{2}}$
C. $640\pi k{{m}^{2}}$
D. $120\pi k{{m}^{2}}$

Answer 1

We are given the height of an antenna and are asked to find the area of coverage. We have an equation to find the total area covered by a tower. By finding the total distance the signal from the antenna reaches and by substituting then in the equation to find total area covered we will get the solution.

Formula used:
$d=\sqrt{2Rh}$
$A=\pi {{d}^{2}}$

Complete step-by-step answer:
In the question we are asked to find the area covered by a transmitting antenna.
The height of the antenna is given to us as 50. If ‘$h$’ is the height of the antenna, then we have
$h=50m$
We know that the maximum distance up to which the signal from an antenna of height ‘h’ reaches is given by the equation,
$d=\sqrt{2Rh}$, were ‘d’ is the maximum distance, ‘R’ is the radius of earth and ‘h’ is the height of the antenna.
We know that the value of radius of earth is,
$R=6.4\times {{10}^{6}}m$
Therefore in the given situation the maximum distance to which the signal from the antenna will reach can be written as,
$d=\sqrt{2\left( 6.4\times {{10}^{6}} \right)50}$
$\Rightarrow d=\sqrt{640\times {{10}^{-6}}}m$
We need to find the total area covered by the transmitting antenna.
We know that the equation for total area covered by the transmitting antenna is given as,
$A=\pi {{d}^{2}}$, were ‘d’ is the total distance.
Since we know,
$d=\sqrt{640\times {{10}^{-6}}}m$
We get,
$\Rightarrow {{d}^{2}}=640\times {{10}^{-6}}m$
Therefore the total area covered will be,
$\Rightarrow A=\pi \times 640\times {{10}^{-6}}{{m}^{2}}$
By converting this into kilometers, we get
$\Rightarrow A=640\pi k{{m}^{2}}$
Therefore the total area covered by the transmitting antenna is $640\pi k{{m}^{2}}$.

So, the correct answer is “Option C”.

Note: Consider an antenna AB of height ‘h’ placed at a point ‘A’ on the surface of the earth as shown in the figure below.

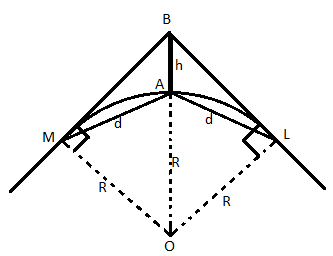
Let ‘O’ be the centre and ‘R’ be the radius of earth.
‘L’ is a point on earth’s surface beyond which the signal from the antenna will not be received.
The distance from ‘A’ to ‘L’ is considered as ‘d’.
From the figure we can see that ‘BL’ is a tangent of earth and height of the antenna is negligible when compared with the range.
Therefore we can say that,
AL = BL = d
Now let us consider the triangle ‘BLO’. We can see that the triangle is a right angled.
By applying Pythagoras theorem we get,
$O{{B}^{2}}=O{{L}^{2}}+B{{L}^{2}}$
From the figure we know that,
$OB=R+h$
$OL=R$
$BL=d$
Therefore,
$\Rightarrow {{\left( R+h \right)}^{2}}={{R}^{2}}+{{d}^{2}}$
By simplifying this, we get
$\Rightarrow {{R}^{2}}+2Rh+{{h}^{2}}={{R}^{2}}+{{d}^{2}}$
$\Rightarrow {{d}^{2}}=2Rh+{{h}^{2}}$
We know that the height of the antenna ‘h’ is very small when compared to the radius of earth. Therefore ‘${{h}^{2}}$’ can be neglected.
Thus,
$\Rightarrow {{d}^{2}}=2Rh$
$\Rightarrow d=\sqrt{2Rh}$
Since area, $A=\pi {{d}^{2}}$
We get area as, $A=2Rh\pi$