Question

The area bounded by $y=x.{{e}^{|x|}}$ and the lines $|x|=1,y=0$ is

& (A)\text{ 1} \\\ & \text{(B) 2} \\\ & \text{(C) 4} \\\ & \text{(D) 6} \\\ \end{aligned}$$

Answer 1

Hint: Initially we have to draw the graph of a given set of equations. We should find the intersection point of the equations in the set. Now, shade the area in the graph as per given set of equations and conditions. As per the shaded area, integrate the equations within given limits. This represents the area bounded by given curves. By using ILATE rule, we can decide which function to be considered as u and which function to be considered as vAs per integration by parts formulae we get $I=\int{uvdx}=u\int{vdx}-\int{\dfrac{du}{dx}\int{vdx}}$.

Complete step-by-step answer:
We are given to find the area bounded by $y=x.{{e}^{|x|}}$ and the lines $|x|=1,y=0$.
We know that |x|=\left\\{ \begin{aligned} & -x,x<0 \\\ & x,x>0 \\\ \end{aligned} \right..........(1)
Hence, y=x.{{e}^{|x|}}=\left\\{ \begin{aligned} & x{{e}^{-x}},x<0 \\\ & x{{e}^{x}},x>0 \\\ \end{aligned} \right.........(2)
From equation (1), it is clear that $|x|=1\Rightarrow x=\pm 1..........(3)$
The equation y=0 represents x-axis.
If x>0, we have to find the area bounded by $y=x{{e}^{x}}$and the lines x=1, y=0.
If x<0, we have to find the area bounded by $y=x{{e}^{-x}}$ and the lines x=-1, y=0.
Case-1: (x>0)
Now, we have to find the intersection point of $y=x{{e}^{x}}$and x=1.
We have to substitute x=1 in $y=x{{e}^{x}}$.
$\Rightarrow y=(1){{e}^{(1)}}=e$
Hence, the intersection point of $y=x{{e}^{x}}$ and x=1 is (1, e).
Case-2: (x<0)
Now, we have to find the intersection point of $y=x{{e}^{x}}$and x=-1.
We have to substitute x=-1 in $y=x{{e}^{-x}}$.
$\Rightarrow y=(-1){{e}^{(1)}}=-e$
Hence, the intersection point of $y=x{{e}^{-x}}$ and x=-1 is (-1, -e).
Now, we have to draw a graph representing all the above conditions.

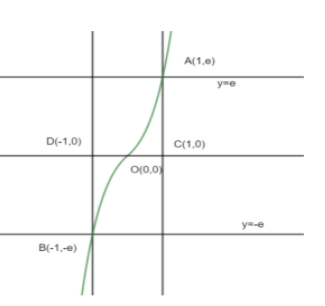
Let us assume O as origin.
Let the intersection of $y=x{{e}^{x}}$and x=1 is A (1.e).
Let the intersection point of $y=x{{e}^{-x}}$ and x=-1 is B (-1, -e).
Let us assume a point C (1,0) and D (-1,0).
Now, we have to choose the area required to calculate.
If x<0, the area required is equal to area bounded by region DOB.
If x>0, the area required is equal to area bounded by region COA.
Hence,
Area bounded by $y=x.{{e}^{|x|}}$ and the lines $|x|=1,y=0$
= Area bounded by region DOB + Area bounded by region COA.
Let us assume
A= Area bounded by $y=x.{{e}^{|x|}}$ and the lines $|x|=1,y=0$
${{A}_{1}}$ = Area bounded by region DOB
${{A}_{2}}$ = Area bounded by region COA
We get $A={{A}_{1}}+{{A}_{2}}$

& {{A}_{1}}=\int\limits_{0}^{1}{(x{{e}^{x}})dx} \\\ & \\\ \end{aligned}$$ Term $${{A}_{1}}$$ can be solved by u-v method. As per integration by parts formula, $$I=\int{uvdx}=u\int{vdx}-\int{\dfrac{du}{dx}\int{vdx}}$$. We know that ILATE rule says us that when we are applying integration by parts formula a certain order is followed how to consider u and how to consider v. In ILATE, I represent integration, L represents logarithmic functions, A represents arithmetic functions, T represents trigonometric functions and E represents exponential functions. We will consider a function as u among the two given functions which comes first in the descending order of ILATE and the other function is considered as v. In this way, we will choose u, v and then we will apply integration by parts formula. As per ILATE rule, Assume $$u=x,v={{e}^{x}}$$ $${{A}_{1}}=\int\limits_{0}^{1}{x{{e}^{x}}dx}=\left[ x\int{{{e}^{x}}dx}-\int{\dfrac{d}{dx}(x)\int{{{e}^{x}}}dx} \right].......(5)$$ We know that $$\int{{{e}^{x}}dx}={{e}^{x}}.......(6)$$ Substitute equation (6) in equation (5) $$\begin{aligned} & \Rightarrow {{A}_{1}}=\left[ x{{e}^{x}}-\int{(1)\int{{{e}^{x}}}dx} \right]_{0}^{1} \\\ & \Rightarrow {{A}_{1}}=\left[ x{{e}^{x}}-{{e}^{x}} \right]_{0}^{1}=(e-e)-(0-1) \\\ & \Rightarrow {{A}_{1}}=1.......(7) \\\ \end{aligned}$$ $${{A}_{2}}=\int\limits_{-1}^{0}{(x{{e}^{-x}})dx}$$ Term $${{A}_{2}}$$ can be solved by u-v method. As per integration by parts formula $$I=\int{uvdx}=u\int{vdx}-\int{\dfrac{du}{dx}\int{vdx}}$$. As per ILATE rule mentioned above, Assume $$u=x,v={{e}^{-x}}$$ $${{A}_{2}}=\int\limits_{0}^{1}{x{{e}^{-x}}dx}=\left[ x\int{{{e}^{-x}}dx}-\int{\dfrac{d}{dx}(x)\int{{{e}^{-x}}}dx} \right].......(6)$$ We know that $$\int{{{e}^{-x}}dx}=-{{e}^{-x}}.......(9)$$ Substitute equation (9) in equation (8) $$\begin{aligned} & \Rightarrow {{A}_{2}}=\left[ -x{{e}^{-x}}-\int{(1)\int{{{e}^{-x}}}dx} \right]_{-1}^{0} \\\ & \Rightarrow {{A}_{2}}=\left[ -x{{e}^{-x}}-{{e}^{-x}} \right]_{-1}^{0}=(0+1)-(1({{e}^{-(-1)}})-{{e}^{1}}) \\\ & \Rightarrow {{A}_{2}}=1......(10) \\\ \end{aligned}$$ Finally, From (7) and (10) $$A={{A}_{1}}+{{A}_{2}}$$ $$\begin{aligned} & \Rightarrow A=1+1 \\\ & \Rightarrow A=2 \\\ \end{aligned}$$ So, Area bounded by $$y=x.{{e}^{|x|}}$$ and the lines $$|x|=1,y=0$$ is equal to 2. Hence, option (B) is correct. Note: We must be careful while considering the region from the graph to calculate the area of a given set of equations. We need to understand how to consider the lower limits and upper limits to integrate the area of the region. A student should have a clear view of considering the upper limits and lower limits. In the function $$y=x.{{e}^{|x|}}$$, we are having $$|x|$$ function. Because of this $$|x|$$ function, we will have different functions at x>0 and at x<0\. If x>0, then the function is $$y=x{{e}^{x}}$$. If x<0, then the function is $$y=x{{e}^{-x}}$$. As the function changes at origin, we will integrate $$y=x{{e}^{x}}$$ from 0 to 1 and $$y=x{{e}^{-x}}$$ from -1 to 0.