Solveeit Logo
Login

Question

Question: The area bounded by \(y=\cos x\) , \(y=x+1\) , \(y=0\) is. A.\(\dfrac{3}{2}\) B.\(\dfrac{2}{3}\...

The area bounded by y=cos⁡xy=\cos x , y=x+1y=x+1 , y=0y=0 is.
A.32\dfrac{3}{2}
B.23\dfrac{2}{3}
C.12\dfrac{1}{2}
D.52\dfrac{5}{2}

Explanation

Solution

Hint: Start by drawing the diagram of the situation given in the figure. Find the area of the required regions by using the formula of area of triangle and area using definite integration. If needed find the intersection points of the curves given in the question as well.

Complete step-by-step answer:
Let us start the solution to the above question by drawing the representative figure of the situation given the question.

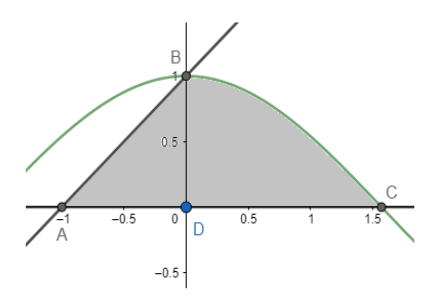
In the figure, the green curve passing through the points B and C is the graph of cosx. Point B is (0,1), as cosx and y=x+1 both pass through the point (0,1). Also, we know that cosx intersects the x-axis at point C(π2,0)C\left( \dfrac{\pi }{2},0 \right) . Point A is the intersection of y=x+1 and y=0 and its coordinates are (-1,0).
Now, we need to find the area of the shaded region. ABD is a triangle with height BD=1unit and base AD=1 unit.
ar(ΔABD)=12×AD×BD=12×1×1=12 unit2ar\left( \Delta ABD \right)=\dfrac{1}{2}\times AD\times BD=\dfrac{1}{2}\times 1\times 1=\dfrac{1}{2}\text{ uni}{{\text{t}}^{2}} .
Now, to find the area of the region BDC, we need to use the method of definite integration. The region is the area bounded by the function y=cosx with the positive x-axis. We know that the area bounded by any general curve y=f(x), in region x=a to x=b is given by ∫abf(x)dx\int\limits_{a}^{b}{f(x)dx} .
ar(BCD)=∫0π2cos⁡xdxar\left( BCD \right)=\int\limits_{0}^{\dfrac{\pi }{2}}{\cos xdx}
Now, we know that the integral of cosx is equal to sinx.
ar(BCD)=∫0π2cos⁡xdx=sin⁡x∣0π2=sin⁡π2−sin⁡0=1 unit2ar\left( BCD \right)=\int\limits_{0}^{\dfrac{\pi }{2}}{\cos xdx}=\sin x|_{0}^{\dfrac{\pi }{2}}=\sin \dfrac{\pi }{2}-\sin 0=1\text{ uni}{{\text{t}}^{2}}
Now, we know that the area of the total region ABC is the sum of the area of BCD and ABD.
∴ar(ABC)=ar(BCD)+ar(ABD)=1+12=32 unit2\therefore ar\left( ABC \right)=ar\left( BCD \right)+ar\left( ABD \right)=1+\dfrac{1}{2}=\dfrac{3}{2}\text{ uni}{{\text{t}}^{2}}
Therefore, the answer to the above question is option (a).

Note: You need to learn all the integrals of the standard functions along with the values of different trigonometric ratios for different standard angles, as they are used very often. Also, learn the graphs of different standard functions, as in such questions, the most important part is the diagram and for drawing the diagram you need to know the curves.