Solveeit Logo
Login

Question

Question: The area bounded by the parabola \({{y}^{2}}=4ax\) and the line \(x=a\And x=4a\) is: (a). \(\dfrac...

The area bounded by the parabola y2=4ax{{y}^{2}}=4ax and the line x=a&x=4ax=a\And x=4a is:
(a). 35a23\dfrac{35{{a}^{2}}}{3}
(b). 4a23\dfrac{4{{a}^{2}}}{3}
(c). 7a23\dfrac{7{{a}^{2}}}{3}
(d). 56a23\dfrac{56{{a}^{2}}}{3}

Explanation

Solution

Hint: First of all write y in terms of x by taking square root on both the sides of the equation y2=4ax{{y}^{2}}=4ax which will give us y=±4axy=\pm \sqrt{4ax}. We know that if we want to get the area under the curve we do the integration so we are going to integrate the expression 4ax\sqrt{4ax} with respect to x and set the lower limit as x=ax=a and upper limit as x=4ax=4a. Now, multiply the answer that you will get after integration by 2 because to get the area under the curve we need to integrate ±4ax\pm \sqrt{4ax} and we have integrated only +4ax+\sqrt{4ax}. The answer of integration of −4ax-\sqrt{4ax} will be the same as +4ax+\sqrt{4ax}.

Complete step-by-step answer:

We need to find the area bounded by the parabola y2=4ax{{y}^{2}}=4ax and the line x=a&x=4ax=a\And x=4a.
The below figure is showing a parabola y2=4ax{{y}^{2}}=4ax and a line x=a&x=4ax=a\And x=4a and CDFE is the bounded region.

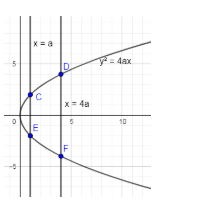
You can see from the above figure that the bounded region of which we have to find the area is CDFE.
We know that if we want to find the area under the curve we will integrate the curve between certain limits as in this problem we are asked to find the area bounded by y2=4ax{{y}^{2}}=4ax and the line x=a&x=4ax=a\And x=4aso we have to integrate the parabola y2=4ax{{y}^{2}}=4ax by converting y in terms of x.
y2=4ax{{y}^{2}}=4ax
Taking square root on both the sides we get,
y=±4axy=\pm \sqrt{4ax}
In the above equation, the “+” sign is showing the curve which lies above x - axis and the “-“sign is showing the curve which lies below x – axis. If you integrate +4ax+\sqrt{4ax} or −4ax-\sqrt{4ax} by setting the limit you will get the same answer so we are going to integrate +4ax+\sqrt{4ax} between the lower limit as x=ax=a and upper limit as x=4ax=4a and multiply the result of this integration by 2.
Integrating y=4axy=\sqrt{4ax} with respect to x between the limits of x=a&x=4ax=a\And x=4a we get,
∫a4aydx=∫a4a4axdx\int\limits_{a}^{4a}{ydx=\int\limits_{a}^{4a}{\sqrt{4ax}}}dx
∫a4aydx=∫a4a4axdx\int\limits_{a}^{4a}{ydx=\int\limits_{a}^{4a}{\sqrt{4a}\sqrt{x}}}dx
We can take the constant 4a\sqrt{4a} out from the integration.
∫a4aydx=4a∫a4axdx\int\limits_{a}^{4a}{ydx=\sqrt{4a}\int\limits_{a}^{4a}{\sqrt{x}}}dx…….. Eq. (1)
We know that the integration of x\sqrt{x} with respect to x is:
∫xdx =x12+112+1=x3232=2x323 \begin{aligned} & \int{\sqrt{x}dx} \\\ & =\dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1}=\dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}}=\dfrac{2{{x}^{\dfrac{3}{2}}}}{3} \\\ \end{aligned}
Substituting this integration value in eq. (1) we get,
∫a4aydx=4a∣2x323∣a4a\int\limits_{a}^{4a}{ydx}=\sqrt{4a}\left| \dfrac{2{{x}^{\dfrac{3}{2}}}}{3} \right|_{a}^{4a}
As 23\dfrac{2}{3} is a constant so we can take 23\dfrac{2}{3} out from the modulus and then plugging the upper limit and the lower limit in the above expression we get,

& \int\limits_{a}^{4a}{ydx}=\sqrt{4a}\dfrac{2}{3}\left| {{\left( 4a \right)}^{\dfrac{3}{2}}}-{{a}^{\dfrac{3}{2}}} \right| \\\ & \Rightarrow \int\limits_{a}^{4a}{ydx}=\sqrt{4a}\dfrac{2}{3}{{a}^{\dfrac{3}{2}}}\left| {{\left( 4 \right)}^{\dfrac{3}{2}}}-{{1}^{\dfrac{3}{2}}} \right| \\\ & \Rightarrow \int\limits_{a}^{4a}{ydx}=2{{a}^{\dfrac{1}{2}+\dfrac{3}{2}}}\dfrac{2}{3}\left| {{\left( 4 \right)}^{\dfrac{3}{2}}}-{{1}^{\dfrac{3}{2}}} \right| \\\ & \Rightarrow \int\limits_{a}^{4a}{ydx}=2{{a}^{2}}\dfrac{2}{3}\left| 8-1 \right| \\\ & \Rightarrow \int\limits_{a}^{4a}{ydx}=2{{a}^{2}}\dfrac{2}{3}\left( 7 \right)=\dfrac{28}{3}{{a}^{2}} \\\ \end{aligned}$$ From the above solution, we have got the integration of $+\sqrt{4ax}$ from $x=a\text{ to }x=4a$ is $\dfrac{28}{3}{{a}^{2}}$. Now, we are going to multiply by 2 then we get $\dfrac{56}{3}{{a}^{2}}$. So, the area bounded by the parabola ${{y}^{2}}=4ax$ and the line $x=a\And x=4a$ is $\dfrac{56}{3}{{a}^{2}}$. Hence, the correct option is (d). Note: In this problem, generally it has observed that in the hastiness of solving problem in exam people forget to multiply the integration of $y=\sqrt{4ax}$ by 2 so before doing this kind of problem always keep in mind that this mistake could happen and kindly check the final answer.