Question

The area bounded by the curve $y = f(x)$, x-axis and the ordinates $x = 1$ and $x = b$ is $(b - 1)\sin (3b + 4)$ then $f(x)$ equals-
A) $(x - 1)\cos (3x + 4)$
B) $\sin (3x + 4)$
C) $\sin (3x + 4) + 3(x - 1)\cos (3x + 4)$
D) None of these.

Answer 1

For solving this particular question we must consider the graph , we have to show the area bounded by the curve $y = f(x)$, x-axis and the ordinates $x = 1$and $x = b$ , then we have to equate the area bounded by the curve to the area given in the question that is $(b - 1)\sin (3b + 4)$. Lastly we have to use newton-leibniz rule for finding the function.

Complete step by step solution:
The area bounded by the curve $y = f(x)$, x-axis and the ordinates $x = 1$ and $x = b$ is ,

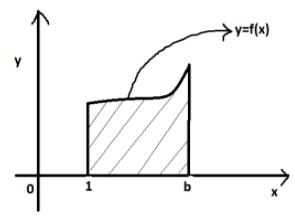
Area is $(b - 1)\sin (3b + 4)$ (given)
We know that the area of the bounded curve is given as ,
$A = \int\limits_1^b {f(x)dx}$
According to the question,
$\Rightarrow \int\limits_1^b {f(x)dx} = (b - 1)\sin (3b + 4)$
Now , applying Newton-leibniz rule , we have a formula which express the value of the given definite integral , let we have the given function that is $f(x)$ and we have to integrate the given function over a definite interval then we can express this as
$\int\limits_a^b {f(x)dx} = F(b) - F(a)$
Therefore, we will get the following ,
$\Rightarrow f(b) - 0 = \sin (3b + 4) + 3(b - 1)\cos (3b + 4) \\\ \Rightarrow f(x) = \sin (3x + 4) + 3(x - 1)\cos (3x + 4) \\\$

Therefore, option $C$ is the correct option.

Formula used:
We have a formula which express the value of the given definite integral , let we have the given function that is $f(x)$ and we have to integrate the given function over a definite interval then we can express this as
$\int\limits_a^b {f(x)dx} = F(b) - F(a)$

Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. You have to use basic definite integral rules. We have to plot the curve according to the question.