Question

The area bounded by the curve $y = \cos x$, the line joining $\left( { - \pi /4,\cos \left( { - \pi /4} \right)} \right)$ and $\left( {0,2} \right)$ and the line joining $\left( { - \pi /4,\cos \left( { - \pi /4} \right)} \right)$ and $\left( {0,2} \right)$ is :
A) $\dfrac{{4 + \sqrt 2 }}{8}\pi - \sqrt 2$
B) $\dfrac{{4 + \sqrt 2 }}{8}\pi + \sqrt 2$
C) $\dfrac{{4 + \sqrt 2 }}{4}\pi - \sqrt 2$
D) $\dfrac{{4 + \sqrt 2 }}{8}\pi + \sqrt 2$

Answer 1

We will first plot the curves and the points using the equation of curve and the points given. We will find the equation of the lines using the points. Then we will find the area under the two lines and the area under the curve and to get the required area, we will subtract the area under the curve from the area under the lines.

Complete Step by Step Solution:
We will first plot the curves and the points.

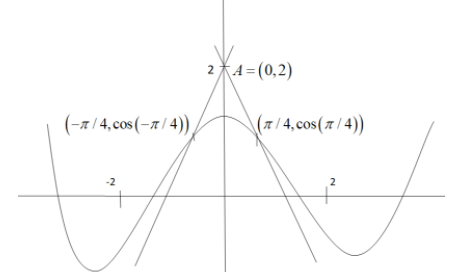
Now, we will find the equation of the line joining the points $\left( { - \pi /4,\cos \left( { - \pi /4} \right)} \right)$ and $\left( {0,2} \right)$ , we know that the equation of the line is given by $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
On substituting all the values of the coordinates of the point in the above formula, we get
$y - 2 = \dfrac{{\cos \left( { - \dfrac{\pi }{4}} \right) - 2}}{{\left( { - \dfrac{\pi }{4}} \right) - 0}}\left( {x - 0} \right)$
On substituting $\cos \left( { - \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$ in the above equation, we get
$\Rightarrow y - 2 = \dfrac{{\dfrac{1}{{\sqrt 2 }} - 2}}{{ - \dfrac{\pi }{4}}}\left( {x - 0} \right)$
On further simplification, we get
$\Rightarrow y - 2 = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x$
On adding 2 on both sides, we get
$\Rightarrow y = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x + 2$ ………… $\left( 1 \right)$
Area under this line can be obtained by integrating the equation of the line. From the graph, points of intersection of this line with the curve are $\left( { - \pi /4,\cos \left( { - \pi /4} \right)} \right)$ and $\left( {0,2} \right)$. So, we need the area under the line in the interval $\left[ { - \dfrac{\pi }{4},0} \right]$ . So, we can find the area as
${A_1} = \int\limits_{ - \dfrac{\pi }{4}}^0 {\left( {\dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x + 2} \right)dx}$
We can this expression as
$\Rightarrow {A_1} = \int\limits_{ - \dfrac{\pi }{4}}^0 {\dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}dx} + \int\limits_{ - \dfrac{\pi }{4}}^0 {2dx}$
On integrating each term by taking constant out of the integration, we get
$\Rightarrow {A_1} = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {\dfrac{{{x^2}}}{2}} \right]_{ - \dfrac{\pi }{4}}^0 + 2\left[ x \right]_{ - \dfrac{\pi }{4}}^0$
On putting the limits of integration, we get
$\Rightarrow {A_1} = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {0 - \dfrac{1}{2}{{\left( { - \dfrac{\pi }{4}} \right)}^2}} \right] + 2\left[ {0 - \left( { - \dfrac{\pi }{4}} \right)} \right]$
On further simplifying the terms, we get
$\Rightarrow {A_1} = \dfrac{\pi }{2} - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right)$ ……… $\left( 2 \right)$
Now, we will find the equation of the line joining the points $\left( {\pi /4,\cos \left( {\pi /4} \right)} \right)$ and $\left( {0,2} \right)$ , we know that the equation of the line is given by $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
On substituting all the values of the coordinates of the point in the above equation, we get
$y - 2 = \dfrac{{\cos \left( {\dfrac{\pi }{4}} \right) - 2}}{{\left( {\dfrac{\pi }{4}} \right) - 0}}\left( {x - 0} \right)$
On substituting $\cos \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$ in the above equation, we get
$\Rightarrow y - 2 = \dfrac{{\dfrac{1}{{\sqrt 2 }} - 2}}{{\dfrac{\pi }{4}}}\left( {x - 0} \right)$
On further simplification, we get
$\Rightarrow y - 2 = - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x$
On adding 2 on both sides, we get
$\Rightarrow y = - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x + 2$ ………… $\left( 3 \right)$
Area under this line can be obtained by integrating the equation of the line. From the graph, points of intersection of this line with the curve are $\left( { - \pi /4,\cos \left( { - \pi /4} \right)} \right)$ and $\left( {0,2} \right)$. So, we need the area under the line in the interval $\left[ {0,\dfrac{\pi }{4}} \right]$ . So, we can find the area as
${A_2} = \int\limits_0^{\dfrac{\pi }{4}} {\left( { - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x + 2} \right)dx}$
We can write this expression as
$\Rightarrow {A_2} = \int\limits_0^{\dfrac{\pi }{4}} { - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}dx} + \int\limits_0^{\dfrac{\pi }{4}} {2dx}$
On integrating each term by taking constant out of the integration, we get
$\Rightarrow {A_2} = - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^{\dfrac{\pi }{4}} + 2\left[ x \right]_0^{\dfrac{\pi }{4}}$
On putting the limits of integration, we get
$\Rightarrow {A_2} = - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {\dfrac{1}{2}{{\left( {\dfrac{\pi }{4}} \right)}^2} - 0} \right] + 2\left[ {\dfrac{\pi }{4} - 0} \right]$
On further simplifying the terms, we get
$\Rightarrow {A_2} = \dfrac{\pi }{2} - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right)$ ……… $\left( 3 \right)$
Now, we will find the area under the curve $y = \cos x$.
Area under this curve is given by
$\Rightarrow {A_3} = \int\limits_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}} {\cos x \cdot dx}$
On integrating the term, we get
$\Rightarrow {A_3} = \left[ {\sin x} \right]_{ - \dfrac{\pi }{4}}^{\dfrac{\pi }{4}}$
On applying the limits, we get
$\Rightarrow {A_3} = \sin \dfrac{\pi }{4} - \sin \left( { - \dfrac{\pi }{4}} \right)$
We know that $\sin \left( { - \dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$ and $\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$.
Thus, we get
$\Rightarrow {A_3} = \dfrac{1}{{\sqrt 2 }} - \left( { - \dfrac{1}{{\sqrt 2 }}} \right)$
On further simplification, we get
$\Rightarrow {A_3} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2$
The required area will be equal to the sum of the area of the lines minus the area of the curve.
Required area $= {A_1} + {A_2} - {A_3}$
On substituting the value of the areas, we get
$\Rightarrow$ Required area $= \dfrac{\pi }{2} - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right) + \dfrac{\pi }{2} - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right) - \sqrt 2$
On further simplifying the terms, we get
$\Rightarrow$ Required area $= \pi - \dfrac{{\left( {2\sqrt 2 - 1} \right)}}{{4\sqrt 2 }}\pi - \sqrt 2$
On taking the factor common, we get
$\Rightarrow$ Required area $= \pi \left( {1 - \dfrac{{\left( {2\sqrt 2 - 1} \right)}}{{4\sqrt 2 }}} \right) - \sqrt 2$
On subtracting the terms, we get
$\Rightarrow$ Required area $= \pi \left( {\dfrac{{4\sqrt 2 - 2\sqrt 2 + 1}}{{4\sqrt 2 }}} \right) - \sqrt 2$
$\Rightarrow$ Required area $= \pi \left( {\dfrac{{2\sqrt 2 + 1}}{{4\sqrt 2 }}} \right) - \sqrt 2$
On multiplying $\sqrt 2$ to numerator and denominator of the first term, we get
$\Rightarrow$ Required area $= \pi \left( {\dfrac{{\left( {2\sqrt 2 + 1} \right)\sqrt 2 }}{{4\sqrt 2 \times \sqrt 2 }}} \right) - \sqrt 2$
$\Rightarrow$ Required area $= \pi \left( {\dfrac{{4 + \sqrt 2 }}{8}} \right) - \sqrt 2$
Hence, the required area is equal to $\dfrac{{4 + \sqrt 2 }}{8}\pi - \sqrt 2$

Therefore, the correct option is option A.

Note:
To solve this problem, we need to remember the basic formulas of integration of many functions. Integration is a method of summing up the discrete data. It is the inverse of differentiation. We need to remember that the area under any curve and straight lines is calculated by using the integration method. We can see that the area that we have obtained is symmetrical about the $y$ axis.