Question

The area bounded by the curve $y = 4x - {x^2}$ and the X-axis, is
A. $\dfrac{{32}}{3}$ sq.unit
B. $\dfrac{{31}}{7}$ sq.unit
C. $\dfrac{{32}}{7}$ sq.unit
D. $\dfrac{{34}}{3}$ sq.unit

Answer 1

Hint : We apply the application of integrals to find the area of the given curve and axis. Equation of X-axis is given by $y = 0$ . By using the given curve and equation of X-axis we find the limits of the integration. Solving the obtained definite integral we obtained the required area of the given region. We can represent the above region in a plane.

Complete step-by-step answer :
Given, the curve $y = 4x - {x^2}$ ---- (1)
As we know the equation of X-axis is $y = 0$ ----- (2)
Substituting equation (2) in equation (1) we get,
$y = 4x - {x^2}$
$\Rightarrow 4x - {x^2} = 0$
$\Rightarrow x(4 - x) = 0$ (Using zero product property)
$\Rightarrow x = 0$ and $x = 4$ .
Using this we draw a diagram to show the region bounded by the curve.

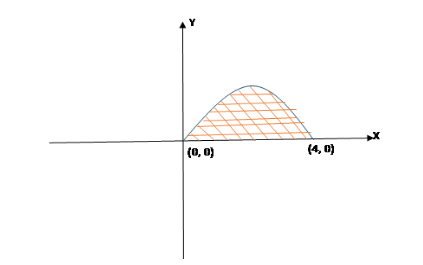
The curve cuts the X-axis at (0, 0) and (4, 0).
So we can see that the limit of x is from 0 to 4.
Hence the required area in the interval [0, 4] is $\int \limits_0^4 {ydx}$ .
$\Rightarrow \int \limits_0^4 {(4x - {x^2})dx}$
Split the integral,
$\Rightarrow \int \limits_0^4 {4xdx - \int \limits_0^4 {{x^2}dx} }$
Take constant outside the integral,
$\Rightarrow 4 \int \limits_0^4 {xdx - \int \limits_0^4 {{x^2}dx} }$
Integrate with respect to x.
$\Rightarrow = 4 \left[ { \dfrac{{{x^2}}}{2}} \right] _0^4 - \left[ { \dfrac{{{x^3}}}{3}} \right] _0^4$
Applying lower and upper limits,
$\Rightarrow \dfrac{4}{2}[{4^2} - 0] - \dfrac{1}{3}[{4^3} - 0]$
$\Rightarrow \dfrac{4}{2}[16 - 0] - \dfrac{1}{3}[64 - 0]$
$\Rightarrow 32 - \dfrac{{64}}{3}$
$\Rightarrow \dfrac{{96 - 64}}{3}$
$\Rightarrow \dfrac{{32}}{3}$ sq.uint.
Hence, the area bounded by the curve $y = 4x - {x^2}$ and the X-axis, is $\dfrac{{32}}{3}$ sq.unit.
So, the correct answer is “Option A”.

Note : Remember that the equation of X-axis is given by $y = 0$ . The equation of Y-axis is given by $x = 0$ . Using the given curve or any equation we find the limits and afterwards we solve it. In the definite integral the integration constant cancels out. Similarly we can find the area bounded by the curves, parabola, circles etc.… In all cases the method is the same as above.