Question

The area bounded by the curve ${\text{y = cosx}}$, the line joining $\left( {\dfrac{{ - \pi }}{4},\cos \left( {\dfrac{{ - \pi }}{4}} \right)} \right)$ and $\left( {0,2} \right)$ and the line joining $\left( {\dfrac{\pi }{4},\cos \left( {\dfrac{\pi }{4}} \right)} \right)$ and $\left( {0,2} \right)$ is :
A) $\dfrac{{4 + \sqrt 2 }}{8}\pi - \sqrt 2$
B) $\dfrac{{4 + \sqrt 2 }}{8}\pi + \sqrt 2$
C) $\dfrac{{4 + \sqrt 2 }}{4}\pi - \sqrt 2$
D) $\dfrac{{4 + \sqrt 2 }}{4}\pi + \sqrt 2$

Answer 1

We can plot the given curves and points. Using the points, we can find the equation of the 2 lines. We can find the area under the lines and the curve by integrating. To find the required area, we must subtract the area under the curve from the area under the line.

Complete step by step solution: Firstly, we can plot the given curves and lines.

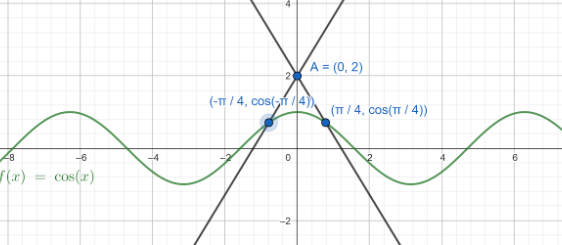
The equation of the line joining the points$\left( {\dfrac{{ - \pi }}{4},\cos \left( {\dfrac{{ - \pi }}{4}} \right)} \right)$ and $\left( {0,2} \right)$ is given by $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
On substituting the values, we get,
$y - 2 = \dfrac{{2 - \cos \left( {\dfrac{{ - \pi }}{4}} \right)}}{{0 - \dfrac{{ - \pi }}{4}}}\left( {x - 0} \right) \\\ y - 2 = \dfrac{{2 - \dfrac{1}{{\sqrt 2 }}}}{{\dfrac{\pi }{4}}} \times x \\\ y - 2 = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x \\\ y = \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x + 2 \\\$
Area under this line is given by integrating the equation of the line. From the graph, points of intersection of the line with other curves are$\left( {\dfrac{{ - \pi }}{4},\cos \left( {\dfrac{{ - \pi }}{4}} \right)} \right)$ and $\left( {{\text{0,2}}} \right)$. So, we need the area under the line in the interval $\left[ {\dfrac{{ - \pi }}{4},0} \right]$. So, we can write,
${A_1} = \int\limits_{\dfrac{{ - \pi }}{4}}^0 {\left( {2 + \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x} \right){\text{ }}} dx \\\ = \int\limits_{\dfrac{{ - \pi }}{4}}^0 {2dx{\text{ }} + } \int\limits_{\dfrac{{ - \pi }}{4}}^0 {\dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x} dx \\\$
On integrating, we get,
$= 2\left[ x \right]_{\dfrac{{ - \pi }}{4}}^0 + \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {\dfrac{{{x^2}}}{2}} \right]_{\dfrac{{ - \pi }}{4}}^0$
On applying the limits, we get,
$= 2 \times \dfrac{\pi }{4} + \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( { - \dfrac{{{\pi ^2}}}{{16}}} \right)$
On further simplification, we get,
$= \dfrac{\pi }{2} - \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right)$
The equation of the line joining the points$\left( {\dfrac{\pi }{4},\cos \left( {\dfrac{\pi }{4}} \right)} \right)$ and $\left( {{\text{0,2}}} \right)$ is given by, $y - {y_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)$
On substituting the values, we get,
$y - 2 = \dfrac{{2 - \cos \left( {\dfrac{\pi }{4}} \right)}}{{0 - \dfrac{\pi }{4}}}\left( {x - 0} \right) \\\ y - 2 = - \dfrac{{2 - \dfrac{1}{{\sqrt 2 }}}}{{\dfrac{\pi }{4}}} \times x \\\$
$y - 2 = - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x \\\ y = 2 - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x \\\$
Area under this line is given by integrating the equation of the line. From the graph, points of intersection of the line with other curves are$\left( {\dfrac{\pi }{4},\cos \left( {\dfrac{\pi }{4}} \right)} \right)$ and $\left( {0,2} \right)$. So, we need the area under the line in the interval $\left[ {{\text{0,}}\dfrac{{\text{}\pi }}{{\text{4}}}} \right]$. So, we can write,
${A_2} = \int\limits_0^{\dfrac{\pi }{4}} {2 - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}x{\text{ }}} dx \\\ = \int\limits_0^{\dfrac{\pi }{4}} {2dx{\text{ }}} - \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}xdx} \\\$
On integrating, we get,
$= 2\left[ x \right]_0^{\dfrac{\pi }{4}} - \dfrac{{4\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^{\dfrac{\pi }{4}}$
On applying the limits, we get,
$= 2 \times \dfrac{\pi }{4} - \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right)$
On further simplification, we get,
$= \dfrac{\pi }{2} - \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right)$
Now we have the curve $y = \cos x$
Area under this curve is given by,
${A_3} = \int\limits_{\dfrac{{ - \pi }}{4}}^{\dfrac{\pi }{4}} {\cos x} dx$
On integrating, we get,
$= \left[ {\sin x} \right]_{\dfrac{{ - \pi }}{4}}^{\dfrac{\pi }{4}}$
On applying the limit, we get,
$= \sin \left( {\dfrac{\pi }{4}} \right) - \sin \left( {\dfrac{{ - \pi }}{4}} \right)$
We know that $\sin \left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$and $\sin \left( {\dfrac{{ - \pi }}{4}} \right) = - \dfrac{1}{{\sqrt 2 }}$. So, we get,
$= \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = \dfrac{2}{{\sqrt 2 }}$
The area of the required region is the sum of the area under the two lines minus the area of the curve $y = \cos x$. It is given by,

$$A = {A_1} + {A_2} - {A_3} \\\ = \dfrac{\pi }{2} - \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right) + \dfrac{\pi }{2} - \dfrac{{2\left( {2\sqrt 2 - 1} \right)}}{{\pi \sqrt 2 }}\left( {\dfrac{{{\pi ^2}}}{{16}}} \right) - \dfrac{2}{{\sqrt 2 }} \\\$$

$= \pi - \dfrac{{\left( {2\sqrt 2 - 1} \right)}}{{4\sqrt 2 }}\pi - \sqrt 2$

$$= \pi \left( {1 - \dfrac{{\left( {2\sqrt 2 - 1} \right)}}{{4\sqrt 2 }}} \right) - \sqrt 2 \\\ = \pi \left( {\dfrac{{4\sqrt 2 - 2\sqrt 2 + 1}}{{4\sqrt 2 }}} \right) - \sqrt 2 \\\ = \pi \left( {\dfrac{{2\sqrt 2 + 1}}{{4\sqrt 2 }}} \right) - \sqrt 2 \\\$$

$= \pi \left( {\dfrac{{4 + \sqrt 2 }}{8}} \right) - \sqrt 2$
Therefore, the required area is $\pi \left( {\dfrac{{4 + \sqrt 2 }}{8}} \right) - \sqrt 2$ square units.

So, the correct answer is option A.

Note: We must draw a graph for better understanding of the question. Equation of line passing through 2 points $\left( {{{\text{x}}_{\text{1}}}{\text{,}}{{\text{y}}_{\text{1}}}} \right)$ and $\left( {{{\text{x}}_{\text{2}}}{\text{,}}{{\text{y}}_{\text{2}}}} \right)$ is given by,
${\text{y - }}{{\text{y}}_{\text{1}}}{\text{ = }}\dfrac{{{{\text{y}}_{\text{2}}}{\text{ - }}{{\text{y}}_{\text{1}}}}}{{{{\text{x}}_{\text{2}}}{\text{ - }}{{\text{x}}_{\text{1}}}}}\left( {{\text{x - }}{{\text{x}}_{\text{1}}}} \right)$.
The area under a curve is given by integration. The limits of integration are the x coordinates of the points of intersection of the curves.
As the whole figure is symmetrical along the y-axis, we can find half of the area and then multiply it.