Question

The area bounded by the curve + = and x² + y² = a², a > 0 is -

• A. sq. units
• B. sq. units
• C. $\left\{ \pi \mathrm { a } ^ { 2 } - \frac { 3 \mathrm { a } ^ { 2 } } { 2 } \right\}$sq. units
• D. None of these

Answer 1

Answer: (A)

sq. units

Answer 2

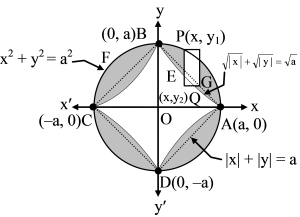
The shaded region in figure represents the region enclosed by x² + y² = a² and . From the symmetry, it is evident that

Required area = 4 [Area of the region bounded by the two curves in first quadrant only]

= 4 = 4dx

= 4

= 4$\left[ \frac { 1 } { 2 } x \sqrt { a ^ { 2 } - x ^ { 2 } + \frac { 1 } { 2 } } a ^ { 2 } \sin ^ { - 1 } \frac { x } { a } - a x - \frac { x ^ { 2 } } { 2 } + \frac { 4 \sqrt { a } } { 3 } x ^ { 3 / 2 } \right] _ { 0 } ^ { a }$

= 4

= sq. units.