Question

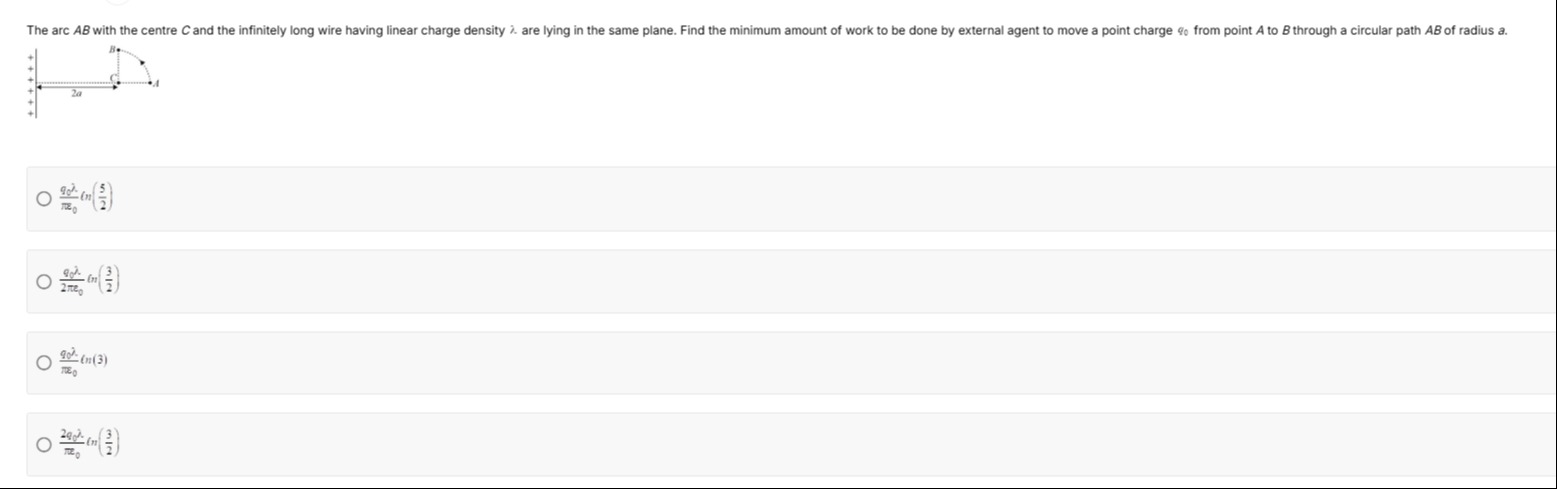
The arc $AB$ with the centre $C$ and the infinitely long wire having linear charge density $\lambda$ are lying in the same plane. Find the minimum amount of work to be done by external agent to move a point charge $q_0$ from point $A$ to $B$ through a circular path $AB$ of radius $a$.

• A. $\frac{q_0\lambda}{\pi\epsilon_0}ln(\frac{5}{2})$
• B. $\frac{q_0\lambda}{2\pi\epsilon_0}ln(\frac{3}{2})$
• C. $\frac{q_0\lambda}{\pi\epsilon_0}ln(3)$
• D. $\frac{2q_0\lambda}{\pi\epsilon_0}ln(\frac{3}{2})$

Answer 1

Answer: (B)

$\frac{q_0\lambda}{2\pi\epsilon_0}ln(\frac{3}{2})$

Answer 2

The work done by an external agent to move a charge $q_0$ from point A to point B is given by $W_{ext} = q_0 (V_B - V_A)$, where $V_A$ and $V_B$ are the electric potentials at points A and B, respectively. The electric potential at a distance $r$ from an infinitely long straight wire with linear charge density $\lambda$ is $V(r) = -\frac{\lambda}{2\pi\epsilon_0} \ln(r) + C'$, where $C'$ is an arbitrary constant.

From the geometry implied by the diagram and the options, we can deduce the distances of points A and B from the wire. Let the wire be along the y-axis ($x=0$). The center of the arc C is at a distance $2a$ from the wire. Point A is located such that its distance from the wire is $r_A = 3a$. Point B is located such that its distance from the wire is $r_B = 2a$.

The potential at A is $V_A = -\frac{\lambda}{2\pi\epsilon_0} \ln(3a) + C'$. The potential at B is $V_B = -\frac{\lambda}{2\pi\epsilon_0} \ln(2a) + C'$.

The work done by the external agent is: $W_{ext} = q_0 (V_B - V_A)$ $W_{ext} = q_0 \left[ \left(-\frac{\lambda}{2\pi\epsilon_0} \ln(2a) + C'\right) - \left(-\frac{\lambda}{2\pi\epsilon_0} \ln(3a) + C'\right) \right]$ $W_{ext} = q_0 \left[ -\frac{\lambda}{2\pi\epsilon_0} \ln(2a) + \frac{\lambda}{2\pi\epsilon_0} \ln(3a) \right]$ $W_{ext} = \frac{q_0\lambda}{2\pi\epsilon_0} \left[ \ln(3a) - \ln(2a) \right]$ Using the logarithm property $\ln x - \ln y = \ln(x/y)$: $W_{ext} = \frac{q_0\lambda}{2\pi\epsilon_0} \ln\left(\frac{3a}{2a}\right)$ $W_{ext} = \frac{q_0\lambda}{2\pi\epsilon_0} \ln\left(\frac{3}{2}\right)$