Question

The angular spread of central maximum, in diffraction pattern, does not depend on _____________
A) The distance between the slit and the source
B) Width of the slit
C) Wavelength of light
D) Frequency of light

Answer 1

This problem can be solved by writing the formula for the path difference for the central maximum in single slit diffraction and then obtaining the formula for the angular width of the central maximum for it. Upon analysis of this formula, we can check upon which factor the angular width does not depend upon.

Formula used:
$\Delta x=d\sin \theta$
$\Delta x=\lambda$

Complete step-by-step answer:
Let us try to get the mathematical formula for the angular width of the central maximum in single slit diffraction.
The path difference $\Delta x$ for a point on the screen in single slit diffraction is
$\Delta x=d\sin \theta$ --(1)
Where $d$ is the width of the slit and $\theta$ is the angle made by the line joining the centre of the slit to the point on the screen to the perpendicular from the plane of the slit towards the screen.

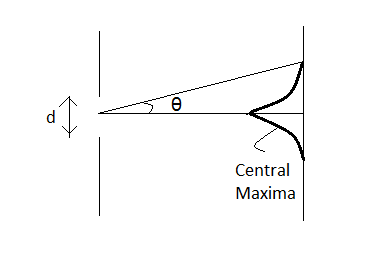
Also, the path difference $\Delta x$ for the central maxima is
$\Delta x=\lambda$ --(2)
where $\lambda$ is the wavelength of light used.
Comparing (1) and (2), we get,
$d\sin \theta =\lambda$
$\therefore \sin \theta =\dfrac{\lambda }{d}$
$\therefore \theta ={{\sin }^{-1}}\left( \dfrac{\lambda }{d} \right)$ --(3)
Now, as is clear from the figure, the central maximum is symmetric on both sides of the central axis. Hence, the angular width $\beta$ of the central maximum will be $2\theta$. Therefore, using (3), we get,
$\beta =2\theta$
$\therefore \beta =2{{\sin }^{-1}}\left( \dfrac{\lambda }{d} \right)$ --(4)
Hence, we can see that the angular width of the central maximum does not depend on the distance between the slit and the source. Hence, the correct option is A) The distance between the slit and the source.

Note: Students might be tempted to think that the frequency of the light can also be the correct answer in this question as it has no mention in equation (4). However, they must remember that the wavelength and frequency of light are related to each other as their product is a constant (the speed of light) and hence, frequency is inversely proportional to the wavelength of light. Therefore, the angular width of the central maximum depends upon the frequency of the light (since it depends upon the wavelength).