Question

The angular speed of Earth in $\text{rad }{{\text{s}}^{-1}}$ so that bodies on equator may appear weightless is [Use $\text{g = 10 m}{{\text{s}}^{-2}}$ and the radius of Earth = $6.4\times {{10}^{3}}\text{ km}$ ]
(A). $1.25\times {{10}^{-3}}$
(B). $1.56\times {{10}^{-3}}$
(C). $1.25\times {{10}^{-1}}$
(D). $1.56$

Answer 1

For a weightless body, the net forces acting on it must be 0. On the equator, the main forces acting on the body are weight and centrifugal force, both in opposite directions and hence cancel each other. So equating the forces to 0 and substituting the corresponding values for Earth will give us the required angular velocity.

Formula used:
${{\text{F}}_{c}}\text{ = }\dfrac{\text{m}{{\text{v}}^{2}}}{\text{r}}$
${{\text{F}}_{\text{c}}}\text{ = m}{{\text{ }\\!\\!\omega\\!\\!\text{ }}^{\text{2}}}\text{R}$
$\text{ }\\!\\!\omega\\!\\!\text{ = }\sqrt{\dfrac{\text{g}}{\text{R}}}$

Complete step-by-step answer:
Angular velocity is the angular displacement covered in unit time. It’s SI unit is $\text{rad }{{\text{s}}^{-1}}$ . It is denoted by $\text{ }\\!\\!\omega\\!\\!\text{ }$ .
$\text{ }\\!\\!\omega\\!\\!\text{ = }\dfrac{\text{ }\\!\\!\theta\\!\\!\text{ }}{\text{t}}$ Here $\text{ }\\!\\!\theta\\!\\!\text{ }$ is angular displacement while $\text{t}$ is time taken.
Centrifugal force is an inertial force acting on a body moving in a circular direction around a fixed point. Its direction is away from the axis of rotation or the fixed point around which the body is rotating. It is given by,
${{\text{F}}_{c}}\text{ = }\dfrac{\text{m}{{\text{v}}^{2}}}{\text{r}}$
Where $\text{m}$ is the mass of body
$\text{v}$ is tangential velocity
$\text{r}$ is the radius of circle of motion
Due to Earth’s spinning motion, we tend to weigh differently at the equator than at the poles because the effect of centrifugal force is more due to which our weight is slightly reduced.

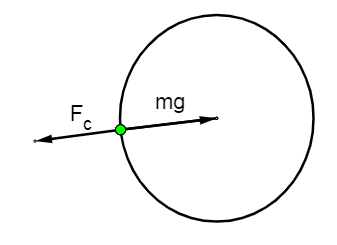
Here${{\text{F}}_{c}}$ is the centrifugal force acting on an object at the equator
${{\text{F}}_{\text{c}}}\text{ = }\dfrac{\text{m}{{\text{v}}^{\text{2}}}}{\text{R}}$ -(1)
converting it in terms of angular velocity,
We know that,
$\text{ }\\!\\!\omega\\!\\!\text{ =}\dfrac{\text{v}}{\text{R}}$
$\Rightarrow \text{v = }\\!\\!\omega\\!\\!\text{ R}$ - (2)
Substituting eq (2) in eq (1) we get,
${{\text{F}}_{\text{c}}}\text{ = m}{{\text{ }\\!\\!\omega\\!\\!\text{ }}^{\text{2}}}\text{R}$
Here $\text{ }\\!\\!\omega\\!\\!\text{ }$ is angular velocity of Earth, $\text{R}$ is radius of Earth.
For a body to be weightless on the equator, the net forces acting on it must be 0. Hence,
$\text{mg - m}{{\text{ }\\!\\!\omega\\!\\!\text{ }}^{\text{2}}}\text{R = 0}$ - (3)
$\text{mg}$ is the weight of the object at equator
Solving eq (3)

& \text{g - }{{\text{ }\\!\\!\omega\\!\\!\text{ }}^{\text{2}}}\text{R = 0} \\\ & \text{g = }{{\text{ }\\!\\!\omega\\!\\!\text{ }}^{\text{2}}}\text{R} \\\ & \Rightarrow \text{ }\\!\\!\omega\\!\\!\text{ = }\sqrt{\dfrac{\text{g}}{\text{R}}} \\\ \end{aligned}$$ Substituting the values of g and R in the above eq, we get, $$ \begin{aligned} & \omega \text{ = }\sqrt{\dfrac{10\text{ m}{{\text{s}}^{-1}}}{6.4\times {{10}^{6}}\text{ m }}} \\\ & \omega \text{ = }\sqrt{\dfrac{{{10}^{-4}}}{64}} \\\ & \omega \text{ = 1}\text{.2}\times \text{1}{{\text{0}}^{-1}}\text{ rad }{{\text{s}}^{-1}} \\\ \end{aligned}$$ Therefore the value of angular velocity of Earth for which object at equator becomes weightless is $$ 1.2\times {{10}^{-1}}\text{ rad }{{\text{s}}^{-1}}$$ . **So, the correct answer is “Option C”.** **Note:** The earth follows two motions- motion around the sun and spinning motion around its axis. The spinning motion or angular velocity of Earth is constant and completes it’s one cycle in 24 hours. It is the reason for day and night and why our day is 24 hours long. The axis on which the Earth rotates is slightly tilted.