Question: The angles shown below are acute and \[\sin ({a^ \circ }) = \cos {b^ \circ }\]. If a=4k-22 and b=6k-...

Question

The angles shown below are acute and $\sin ({a^ \circ }) = \cos {b^ \circ }$ . If a=4k-22 and b=6k-13, what is the value of k? Note that the figures are not drawn to scale.

Answer 1

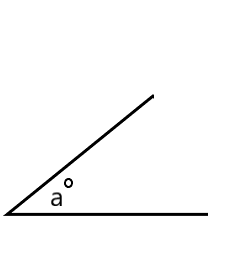
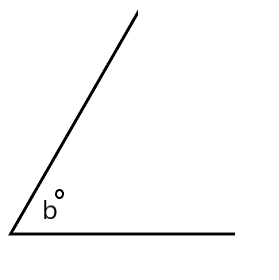
Solution

According to the question, we will first find out ‘b’. Then, we will solve the two equations given in the question in terms of ‘a’ and ‘b’ only, and try to cancel out ‘k’. Then, we will find out the value of ‘a’ and then together put the value of ‘a’ and ‘b’ to find ‘k’.

Formula used: $\sin a = \cos (90 - a)$

Complete step by step answer:
Given is $\sin ({a^ \circ }) = \cos {b^ \circ }$ . Now, we will consider this as equation (1).
We know that $\sin a = \cos (90 - a)$ . Here, we will consider this equation as equation (2).
After comparing both the equations (1) and (2), we get that:
$b = (90 - a)$
We will consider this as equation (3). This equation is important and will be used further.
From the question, we were given two equations:
$a = 4k - 22{\text{ and }}b = 6k - 13$
We will solve these two equations, so that the variable ‘k’ gets cancelled out from both the equations, and we get the equation in terms of ‘a’ and ‘b’. So, we will consider the first equation that is $a = 4k - 22$ as equation (i) and the second one as equation (ii). Now we will multiply equation (i) with 3 and equation (ii) with $2$ , so that we cancel out the common terms:
$\;\;\;3a = 12k - 66 \\\ \;\underline \;\;2b = 12k - 26 \\\ \- \;\;\;\;\; - \;\;\;\;\;\; + \\\ \\\ \;\;\;3a - 2b = - 40 \\\$
We can also write it as:
$2b - 3a = 40$
Now, we will put the value of ‘b’ from equation (1), and we get:
$\Rightarrow 2(90 - a) - 3a = 40$
We will further solve this to get the value of ‘a’, and we get:
$\Rightarrow 180 - 2a - 3a = 40$
$\Rightarrow 180 - 5a = 40$
$\Rightarrow 5a = 140$
$\Rightarrow a = 28$
Now, we will put the value of ‘a’ in equation (i) and we will get the value of ‘k’:
$a = 4k - 22$
$\Rightarrow 28 = 4k - 22$
$\Rightarrow 28 + 22 = 4k$
$\Rightarrow 4k = 50$
$\Rightarrow k = \dfrac{{50}}{4}$
$\Rightarrow k = 12.5$

Therefore, the value of ‘k’ is $12.5$ .

Note: The above method was very easy, but there is another method. If both the angles are given acutely and both the equations are given, then we can add both the equations directly and equate it to 90, because the angles are acute and so equation (1) + equation (2) = 90. Solving this equation, we will get the value of ‘k’.