Question

The angles of elevations of the top of a tower as observed from a point on the ground is $\alpha$ and on moving on ‘a’ meters towards the tower, the angle of elevation is $\beta$. Prove that the height of the tower is $\dfrac{{a\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

Answer 1

We use the concept of angle of elevation and draw a diagram that shows the ‘a’ meters displacement and the angle of elevation before and after the displacement. Assume the remaining distance after the displacement of ‘a’ meters between the tower and the observer as a variable. Apply tangent of each angle of elevation and form two equations for the value of the same variable.

• In a right angled triangle, tan of an angle is given by dividing perpendicular of triangle by base of triangle.

Complete step-by-step solution:
We draw a diagram where we have a tower and observer at a distance.

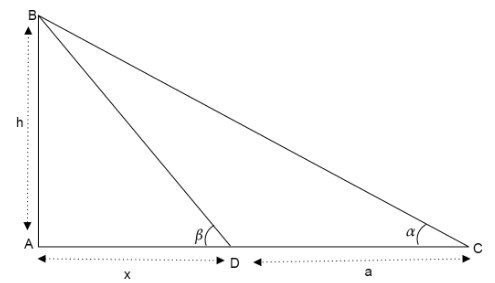
Here AB is the height of the tower i.e. $AB = h$ and the observer makes an angle of elevation $\alpha$ at point C and after proceeding ‘a’ meters towards the tower, makes an angle of elevation $\beta$ at point D.
Let us assume the distance left between the tower and the observer after moving ‘a’ meters closer to the tower as ‘x’.
Since the tower is perpendicular to the ground, then we can say triangle ABC is a right angled triangle.
Now we know $\tan \alpha =$ Perpendicular divided by base
In $\vartriangle ABC$,
$\Rightarrow \tan \alpha = \dfrac{{AB}}{{AC}}$
Substitute the value of $AB = h$ and $AC = AD + CD$
$\Rightarrow \tan \alpha = \dfrac{h}{{AD + CD}}$
Substitute the value of $AD = x;CD = a$ in the denominator
$\Rightarrow \tan \alpha = \dfrac{h}{{x + a}}$
Cross multiply the values from RHS to LHS
$\Rightarrow x + a = \dfrac{h}{{\tan \alpha }}$
Shift ‘a’ to RHS of the equation
$\Rightarrow x = \dfrac{h}{{\tan \alpha }} - a$...................… (1)
Since the tower is perpendicular to the ground, then we can say triangle ABD is a right angled triangle.
Now we know $\tan \beta =$ Perpendicular divided by base
In$\vartriangle ABD$,
$\Rightarrow \tan \beta = \dfrac{{AB}}{{AD}}$
Substitute the value of $AB = h$ and $AD = x$
$\Rightarrow \tan \beta = \dfrac{h}{x}$
Cross multiply the values from RHS to LHS
$\Rightarrow x = \dfrac{h}{{\tan \beta }}$..................… (2)
Equate the value of ‘x’ from both the equations (1) and (2)
$\Rightarrow \dfrac{h}{{\tan \alpha }} - a = \dfrac{h}{{\tan \beta }}$
Take LCM in LHS of the equation
$\Rightarrow \dfrac{{h - a\tan \alpha }}{{\tan \alpha }} = \dfrac{h}{{\tan \beta }}$
Cross multiply the values from both sides of the equation to opposite sides of the equation
$\Rightarrow \tan \beta \left( {h - a\tan \alpha } \right) = h\tan \alpha$
Open the bracket in LHS
$\Rightarrow h\tan \beta - a\tan \alpha \tan \beta = h\tan \alpha$
Bring all terms with constant ‘h’ along with them to LHS of the equation and move rest of the terms to RHS of the equation
$\Rightarrow h\tan \beta - h\tan \alpha = a\tan \alpha \tan \beta$
Take ‘h’ common in LHS of the equation
$\Rightarrow h\left( {\tan \beta - \tan \alpha } \right) = a\tan \alpha \tan \beta$
Divide both sides of the equation by $\left( {\tan \beta - \tan \alpha } \right)$
$\Rightarrow \dfrac{{h\left( {\tan \beta - \tan \alpha } \right)}}{{\left( {\tan \beta - \tan \alpha } \right)}} = \dfrac{{a\tan \alpha \tan \beta }}{{\left( {\tan \beta - \tan \alpha } \right)}}$
Cancel same terms from numerator and denominator in LHS
$\Rightarrow h = \dfrac{{a\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

$\therefore$The height of the tower is equal to $\dfrac{{a\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}$

Note: Students many times make mistake of cancelling the term ‘h’ from both sides of the equation when we equate both values of same variable, this is wrong procedure as we have ‘h’ only in one term in LHS, we will have to take LCM and then check for cancellation. Also, students might try to solve this by applying Pythagoras theorem but that will only give us the equation of hypotenuse and here we have to focus on the height of the tower.