Question
Question: The angles of elevation of the top of a building and the top of the chimney on the roof of the build...
The angles of elevation of the top of a building and the top of the chimney on the roof of the building from a point on the ground are x and 45o respectively. The height of the building is h meter. Then the height of the chimney, in meter is:
(a) h cot x + h
(b) h cot x – h
(c) h tan x – h
(d) h tan x + h
Solution
Hint: To solve this question, we will assume that the height of the chimney be ‘y m’. Also, we will assume that the distance of the point from where things are being observed from the building is ‘p m’. Now, according to the data given in the question, we will form two equations with the two unknown variables (x and p) and then we will solve it by substitution method.
Complete step-by-step answer:
The rough sketch of all the things as mentioned in the question is given below.
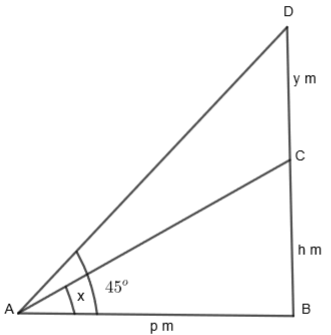
So, we can see from the figure that the point from which all the things have been observed is A. The height of the building is BC = h m. The height of the chimney is y m. And the horizontal distance of both the chimney and the building from point A is p m. The angle of elevation of the top of the building = ∠CAB and the angle of elevation of the top of the chimney is ∠DAB.
Now, we will consider the triangle ABC. Triangle ABC is a right-angled triangle. In the right-angled triangle XYZ, we can say that,
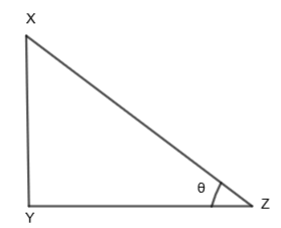
tanθ=YZXY
Thus, in triangle ABC, we can say that,
tan(∠CAB)=ABBC
Here, we know that, ∠CAB=x, BC = h m and AB = p m. So, we will get the following equation.
⇒tanx=ph....(i)
Now, we will consider the triangle ABD. Similarly, from the above, we can say that,
tan(∠DAB)=ABDB
⇒tan45o=ABDB
We know that tan45o=1. So, we get,
⇒1=ABDB
⇒AB=DB
⇒DB=p m
Now, DB = DC + BC. So, we will get,
⇒DC+CB=p
⇒y+h=p...(ii)
From equation (i), we have,
tanx=ph
⇒p=tanxh
⇒p=hcotx....(iii)
Substituting the value of p from (iii) to (ii), we will get,
⇒y+h=hcotx
⇒y=hcotx−h
Thus the height of the chimney = h cot x – h
Hence, option (b) is the right answer.
Note: In this question, we are not given whether the horizontal distance from A to the building and chimney are the same or not. Here, we have assumed that the distance of A to the building and distance of A to the chimney are the same horizontally. If we don’t assume this, then we will get an extra variable in the final answer which we do not desire.
