Question

The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be ${45^ \circ }$ and ${30^ \circ }$ respectively. If the ships are $200{\text{m}}$ apart, find the height of the light house.

Answer 1

Hint : We are asked to find the height of the light house. Draw a diagram for the problem using the given parameters. Observe the diagram carefully. Recall the concepts of a right angled triangle and use them to find the height of the light house with the given angles.

Complete step-by-step answer :
Given, the angles of depression of two ships from the top of a lighthouse on the same side of it are ${\theta _1} = {45^ \circ }$ and ${\theta _2} = {30^ \circ }$ respectively
Distance between the two ships is $d = 200{\text{m}}$ .
Let us first draw a diagram for the problem

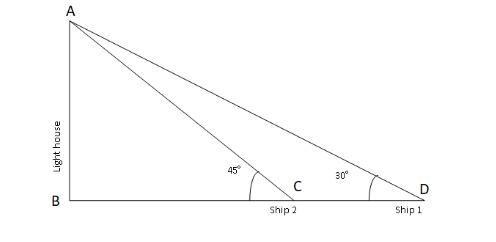
Here, $AB$ is the height of the lighthouse and $CD$ is the distance between the two ships which is given as $200{\text{m}}$ . Therefore, $CD = 200{\text{m}}$
We observe from the figure that there are two right angled triangles which are $\Delta ABC$ and $\Delta ABD$ .
And for right angled triangle we have,
$\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$
where $\theta$ is the angle opposite the perpendicular side
We will use this concept for angles ${45^ \circ }$ and ${30^ \circ }$ in triangles $\Delta ABC$ and $\Delta ABD$ respectively.
For $\Delta ABC$ , we have
$\tan {45^ \circ } = \dfrac{{AB}}{{BC}}$
$\Rightarrow 1 = \dfrac{{AB}}{{BC}}$
$\Rightarrow BC = AB$ (i)
For $\Delta ABD$ , we have
$\tan {30^ \circ } = \dfrac{{AB}}{{BD}}$ (ii)
$BD$ can be written as,
$BD = BC + CD$
Putting the value of $CD$ we get,
$BD = BC + 200$ (iii)
Using equation (iii) in equation (ii) we get,
$\tan {30^ \circ } = \dfrac{{AB}}{{BC + 200}}$
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{BC + 200}}$
$\Rightarrow BC + 200 = \sqrt 3 AB$ (iv)
Using equation (i) in (iv) we get,
$AB + 200 = \sqrt 3 AB$
$\Rightarrow \sqrt 3 AB - AB = 200$
$\Rightarrow AB(\sqrt 3 - 1) = 200$
$\Rightarrow AB = \dfrac{{200}}{{(\sqrt 3 - 1)}}{\text{m}}$
Therefore, the height of the light house will be $\dfrac{{200}}{{(\sqrt 3 - 1)}}{\text{m}}$ .
So, the correct answer is “ $\dfrac{{200}}{{(\sqrt 3 - 1)}}{\text{m}}$ ”.

Note : By angle of depression it means the downward angle from the horizontal line to the point of interest and angle of elevation means the upward angle from the horizontal line to the point of interest. Students usually get confused between the two terms, so always remember their difference.