Question

The angles of depression of the top and bottom of 8m tall building from the top of a multi – storeyed building are ${{30}^{\circ }}$and ${{45}^{\circ }}$respectively. Find the height of the multi – storeyed building and the distance between the two buildings.

Answer 1

Hint: Draw a rough figure of both buildings and make the angles of depression. Consider the triangle is ${{30}^{\circ }}$ and find the height of the multi – storeyed building from the top of the building. Similarly, consider a triangle where angle is ${{45}^{\circ }}$and find the distance between the 2 buildings.

Complete step-by-step answer:
Given the height of the building, AB = 8m.

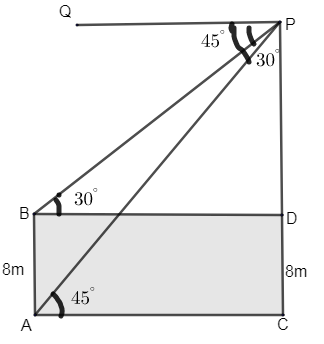
Let us consider the height of the multi – storeyed building = PC.
The distance between the two buildings is taken as AC.
Now, the angle of depression of the top of building is given by,
$\angle QPB={{30}^{\circ }}$[From the figure]
The angle of depression of bottom of the building is given as,
$\angle QPA={{45}^{\circ }}$[From figure]
We have to find the value of AC i.e. the distance and PC, the height of the building.
We have drawn here BD parallel to PQ. i.e. BD || PQ.
Here lines PQ and BD are parallel, and BP becomes the transversal.
$\therefore \angle PBD=\angle QPB={{30}^{\circ }}$, they are alternate angles.
Similarly, PQ is parallel to AC, PQ || AC and AP is the transversal.
$\therefore \angle PAC=\angle QPA={{45}^{\circ }}$, they are alternate angles.
We know AC and BD are parallel lines, thus we can say that the length AC is equal to length of BD.
AC = BD.
Similarly, AB and CD are parallel lines. So, CD = AB.
We know that, AB = 8m.
$\therefore$CD = AB = 8m.
Hence, CD = 8m.
From the figure, we can say that, $PC\bot AC$.
$\therefore \angle PDB=\angle PCA={{90}^{\circ }}$.
Let us first consider the right triangle PBD.
We know, $\tan B$= side opposite to angle B/ side adjacent to angle B.
$\therefore \tan B=\dfrac{PD}{BD}$
Here, angle is ${{30}^{\circ }}$, $\tan B=\dfrac{1}{\sqrt{3}}$, from the trigonometric table.

& \therefore \tan {{30}^{\circ }}=\dfrac{PD}{BD}=\dfrac{1}{\sqrt{3}} \\\ & \therefore BD=PD\sqrt{3}-(1) \\\ \end{aligned}$$ Now let us consider the right triangle PAC. We know, $$\tan {{45}^{\circ }}$$= side opposite to angle A/ side adjacent to angle A. $$\therefore \tan {{45}^{\circ }}=\dfrac{PC}{AC}$$ From the trigonometric table, we know that, $$\tan {{45}^{\circ }}=1$$. $$\begin{aligned} & 1=\dfrac{PC}{AC} \\\ & \Rightarrow AC=PC \\\ \end{aligned}$$ We know that, AC = BD. $$\therefore BD=PC-(2)$$ From (1) and (2), we can equate the values of BD. $$\begin{aligned} & \therefore PC=PD\sqrt{3} \\\ & PD\sqrt{3}=PD+DC [\because CD=8m] \\\ & PD\sqrt{3}=PD+8 \\\ & PD\sqrt{3}-PD=8 \\\ & PD\left( \sqrt{3}-1 \right)=8 \\\ & \therefore PD=\dfrac{8}{\left( \sqrt{3}-1 \right)} \\\ \end{aligned}$$ Now let us rationalize the above expression. Multiply and divide by $$\left( \sqrt{3}-1 \right)$$. $$\therefore PD=\dfrac{8}{\left( \sqrt{3}-1 \right)}\times \dfrac{\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}+1 \right)}$$ We know, $$\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$$. $$\begin{aligned} & PD=\dfrac{8\left( \sqrt{3}+1 \right)}{{{\left( \sqrt{3} \right)}^{2}}-{{1}^{2}}}=\dfrac{8\left( \sqrt{3}+1 \right)}{3-1} \\\ & PD=\dfrac{8\left( \sqrt{3}+1 \right)}{2}=4\left( \sqrt{3}+1 \right) \\\ & \therefore PD=4\left( \sqrt{3}+1 \right) \\\ \end{aligned}$$. We know that, PC = PD + CD. $$\begin{aligned} & \therefore PC=4\left( \sqrt{3}+1 \right)+8 \\\ & PC=4\sqrt{3}+4+8 \\\ & PC=4\sqrt{3}+12 \\\ \end{aligned}$$ $$PC=4\left( \sqrt{3}+3 \right)m$$. So we got the height of the multi – storeyed building = $$PC=4\left( \sqrt{3}+3 \right)m$$. We found out that, AC = BD. We know that, $$BD=PD\sqrt{3}$$. $$\therefore AC=PD\sqrt{3}$$. We know, $$PD=4\left( \sqrt{3}+1 \right)$$. $$\begin{aligned} & \therefore AC=4\left( \sqrt{3}+1 \right)\sqrt{3} \\\ & AC=4\times 3+4\sqrt{3} \\\ & AC=4\sqrt{3}+12 \\\ \end{aligned}$$ $$AC=4\left( \sqrt{3}+3 \right)m$$. Hence, we got the distance between 2 buildings as $$4\left( \sqrt{3}+3 \right)m$$. $$\therefore $$The height of multi – storeyed building = $$4\left( \sqrt{3}+3 \right)m$$ The distance between the two buildings = $$4\left( \sqrt{3}+3 \right)m$$ Note: We have been given the angle of depression which are the angles from top of the multi – storeyed building to the top and bottom of the smaller building. But as they are parallel, it can become alternate angles. So the elevation from top and bottom of the building to multi – storey becomes $${{45}^{\circ }}$$and $${{30}^{\circ }}$$.