Question

The angles of a triangle are in A.P and the least angle is ${{30}^{o}}$. What is the greatest angle (in radian)?
(a) $\dfrac{\pi }{2}$
(b) $\dfrac{\pi }{3}$
(c) $\dfrac{\pi }{4}$
(d) $\pi$

Answer 1

Hint: First of all, we know that the general terms of A.P are like a, a + d, a + 2d…..So, first, assume the angles of the triangle as ${{30}^{o}},\text{ }{{30}^{o}}+d,\text{ }{{30}^{o}}+2d$. Equate the sum of these angles to ${{180}^{o}}$ and get the value of d. Use the value of d to find the greatest angle.

Complete step-by-step answer:

We are given that the angles of the triangle are in A.P and the least angle is ${{30}^{o}}$. We have to find the greatest angle (in radian). Let us first see what arithmetic progression is. Arithmetic Progression (A.P) is a sequence of numbers so that the difference of any two successive numbers is a constant value. For example, the series of natural numbers: 1, 2, 3, 4, 5, 6…. are in A.P with the first term as 1 and common difference as 1. Also, the nth term of A.P is ${{a}_{n}}=a+\left( n-1 \right)d$ where ‘a’ is the first term, and ‘d’ is the common difference.

So, we know that the general terms of any arithmetic progression (A.P) are in the form a, a + d, a + 2d, a + 3d…….Here, ‘a’ is the first term and ‘d’ is the common difference of A.P. We are given that the least angle of the triangle is ${{30}^{o}}$ and all three angles are in A.P. So, let us assume the other two angles as ${{30}^{o}}+d$ and ${{30}^{o}}+2d$. So, we get 3 angles of the triangle as, ${{30}^{o}},\text{ }{{30}^{o}}+d,\text{ }{{30}^{o}}+2d$

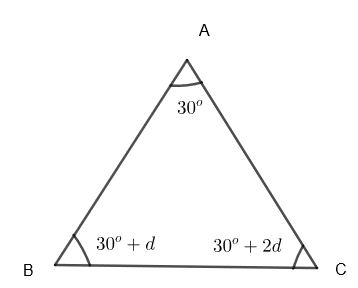
Also, we know that in any triangle, the sum of each of the angles is ${{180}^{o}}$. So, we get, $\angle A+\angle B+\angle C={{180}^{o}}$

By substituting the values of $\angle A,\text{ }\angle B\text{ and }\angle C$, we get, ${{90}^{o}}+3d={{180}^{o}}$
$\Rightarrow 3d={{180}^{o}}-{{90}^{o}}$
$3d={{90}^{o}}$
By dividing 3 on both the sides, we get, $d=\dfrac{{{90}^{0}}}{3}={{30}^{o}}$
So, we get 3 angles of the triangle as,

& \angle A={{30}^{o}} \\\ & \angle B={{30}^{o}}+d={{30}^{o}}+{{30}^{o}}={{60}^{o}} \\\ & \angle C={{30}^{o}}+2d={{30}^{o}}+2\left( {{30}^{o}} \right)={{90}^{o}} \\\ \end{aligned}$$ So, we get the greatest angle as $${{90}^{o}}$$. To get this angle in radian, we will multiply it with $$\dfrac{\pi }{{{180}^{o}}}$$. So, we get, Greatest Angle $$={{90}^{o}}\times \dfrac{\pi }{{{180}^{o}}}=\dfrac{\pi }{2}$$ Hence, option (a) is the right answer. Note: In this question, students often take three angles in the arithmetic progression (A.P) as $$\left( {{30}^{o}}-d \right),{{30}^{o}},\left( {{30}^{o}}+d \right)$$ but this is wrong because it is given in the question that the least angle is $${{30}^{o}}$$. So we must start writing the terms with $${{30}^{o}}$$. Also, the sum of all the angles of the triangle is $${{180}^{o}}$$, but in the above case, as we can see that $$\left( {{30}^{o}}-d \right)+\left( {{30}^{o}} \right)+\left( {{30}^{o}}+d \right)={{90}^{o}}$$ which is incorrect. So, this point must be taken care of and take the 3 angles in A.P as $$\left( {{30}^{o}} \right),\left( {{30}^{o}}+d \right)\text{ and }\left( {{30}^{o}}+2d \right)$$.