Question

The angles in a right-angled isosceles triangle are:
${\text{A}}{\text{. 90}}^\circ ,30^\circ ,60^\circ \\\ {\text{B}}{\text{. 90}}^\circ ,20^\circ ,70^\circ \\\ {\text{C}}{\text{. 90}}^\circ ,40^\circ ,50^\circ \\\ {\text{D}}{\text{. 90}}^\circ ,45^\circ ,45^\circ \\\$

Answer 1

Hint: According to properties of triangles, the sum of angles in a triangle is 180$^\circ$. Since it is a right angles triangle, one angle is 90$^\circ$. The other two angles are equal because it is isosceles.

Complete step-by-step answer:

Given Data, it is a right-angled isosceles triangle.

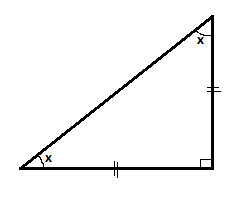
In an isosceles triangle two sides are equal.
Therefore, the angles opposite to both the respective sides are equal.
Let that angle be x.
It is a right angled triangle. Hence one of the angle is 90°.
We know that the sum of angles in a triangle is 180°.
So, 90° + 2x = 180°
⟹2x = 90°
⟹x = 45°

Each of the other angles is 45°.

Hence the angles in a right-angled isosceles triangle are 90°, 45° and 45°.
Option D is the correct answer.

Note: In order to solve this type of questions, the key is to remember that the sum of angles in a triangle is 180° and in a right-angled isosceles triangle one of the angles is 90° and the other two angles are equal. We correlate all these properties to determine the answer.