Question
Question: The angle of refraction in glass is \({30^0}\) when a ray of light passing through air is incident o...
The angle of refraction in glass is 300 when a ray of light passing through air is incident on a plane glass surface at 600. The same ray incident at the same angle on a liquid surface is refracted through 450. What is the angle of refraction when this ray passing through the liquid is incident on the glass surface at 450
Solution
Velocity of light will be different in different media. If velocity of light is higher in one medium and lesser in another medium then the first one is called a rarer medium and the second one is called denser medium. There is a law called snell’s law which relates the refractive indices of the media.
Formula used:
μisini=μrsinr
Complete step by step answer:
Velocity is nothing but the rate of change of displacement i.e the ratio of displacement to the time taken. So the time taken will be displacement upon the velocity.
Velocity of light in any medium of refractive index(n) will be
v=nc where ‘c’ is the velocity of light in the free space and ‘n’ is the refractive index of the medium.
For air, the refractive index will be one. For glass, the refractive index will be greater than one. Hence when light enters from air to glass, its velocity decreases. In order to maintain the same time displacement also must decrease. That means the path travelled in the air by the light must decrease. This will be possible if the light bends towards the normal. Hence the incident angle and the refracted angle will be different. They are related with refractive indices and given by snell’s law.
μisini=μrsinr
Where μi is the refractive index of incident medium and μr is the refractive index of refracted medium. i is the incident angle and r is the refracted angle.
The air refractive index is one.
For air to slab refraction shown below we apply snell's law to get a glass refractive index.
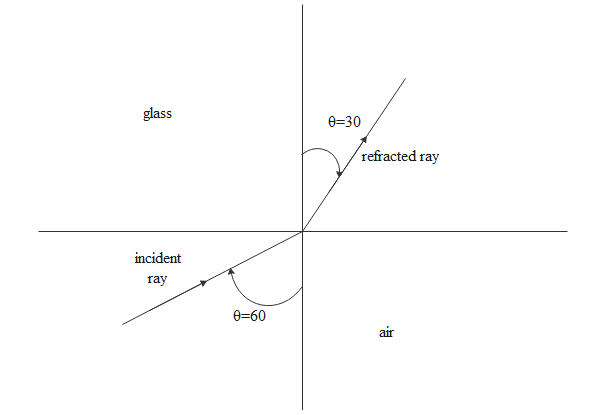
μisini=μrsinr
\eqalign{
& \Rightarrow 1\sin 60 = {\mu _g}\sin 30 \cr
& \Rightarrow {\mu _g} = \dfrac{{\sin 60}}{{\sin 30}} \cr
& \Rightarrow {\mu _g} = \sqrt 3 \cr}
For air liquid interaction shown below we have
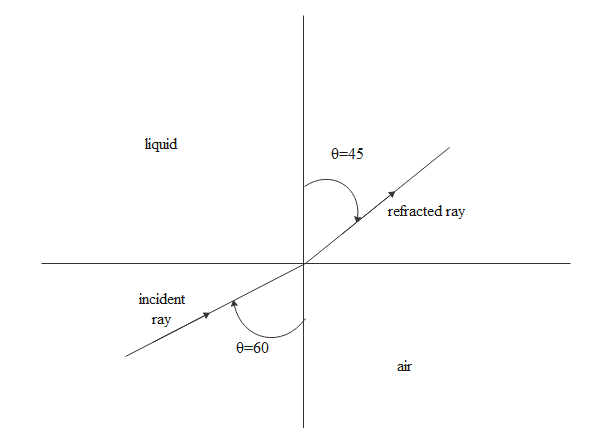
μisini=μrsinr
\eqalign{
& \Rightarrow 1\sin 60 = {\mu _l}\sin 45 \cr
& \Rightarrow {\mu _l} = \dfrac{{\sin 60}}{{\sin 45}} \cr
& \therefore {\mu _l} = \dfrac{{\sqrt 6 }}{2} \cr}
For liquid glass interaction we have
μisini=μrsinr
\eqalign{
& \Rightarrow {\mu _l}\sin 45 = {\mu _g}\sin r \cr
& \Rightarrow \sin r = \dfrac{{{\mu _l}\sin 45}}{{{\mu _g}}} \cr
& \Rightarrow \sin r = \dfrac{{\dfrac{{\sqrt 6 }}{2}\sin 45}}{{\sqrt 3 }} \cr
& \Rightarrow \sin r = \dfrac{1}{2} \cr
& \therefore r = {30^0} \cr}
Hence angle of refraction at glass surface will be 30 degrees.
Note:
Actually when there is a change in the velocity when light enters the different medium, there will be change in the length travelled too, because let us assume the light entered the rarer medium, then the velocity of light increases and the light will bend away from the normal so that the distance travelled also increases so that the time will be constant. One more thing to be remembered is that the refractive index of any medium can’t be less than one.
